题目内容
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.

【答案】(1)见解析(2)![]()
【解析】分析:(1)如图,欲证明EF与⊙O相切,只需证得OD⊥EF.
(2)通过解直角△AEF可以求得AF=10.设⊙O的半径为r,由平行线分线段成比例得到![]() ,即
,即![]() ,则易求AB=AC=2r=
,则易求AB=AC=2r=![]() ,所以EB=AB﹣AE=
,所以EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.
详解:(1)证明:如图,连接OD.
∵OC=OD,∴∠OCD=∠ODC.
∵AB=AC,∴∠ACB=∠B,∴∠ODC=∠B,∴OD∥AB,∴∠ODF=∠AEF.
∵EF⊥AB,∴∠ODF=∠AEF=90°,∴OD⊥EF.
∵OD是⊙O的半径,∴EF与⊙O相切;
(2)由(1)知,OD∥AB,OD⊥EF.
在Rt△AEF中,sin∠CFD=![]() ,AE=6,则AF=10.
,AE=6,则AF=10.
∵OD∥AB,∴![]() .
.
设⊙O的半径为r,∴![]() ,解得:r=
,解得:r=![]() ,∴AB=AC=2r=
,∴AB=AC=2r=![]() ,∴EB=AB﹣AE=
,∴EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.
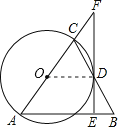

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目