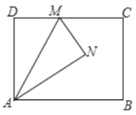
题目内容
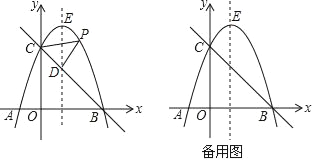
【题目】有一根直尺短边长![]() ,长边长
,长边长![]() ,还有一块锐角为45°的直角三角形纸板,它的斜边长为
,还有一块锐角为45°的直角三角形纸板,它的斜边长为![]() .如图1,将直尺的短边
.如图1,将直尺的短边![]() 与直角三角形纸板的斜边
与直角三角形纸板的斜边![]() 重合,且点
重合,且点![]() 与点
与点![]() 重合.将直尺沿射线
重合.将直尺沿射线![]() 方向平移,如图2,设平移的长度为
方向平移,如图2,设平移的长度为![]() ,且满足
,且满足![]() ,直尺和三角形纸板重叠部分的面积为
,直尺和三角形纸板重叠部分的面积为![]() .
.
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
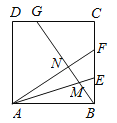
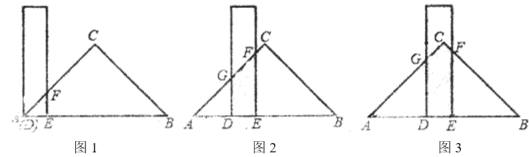
(2)当![]() 时(如图3),请用含
时(如图3),请用含![]() 的代数式表示
的代数式表示![]() .
.
(3)是否存在一个位置,使重叠部分面积为![]() ?若存在求出此时
?若存在求出此时![]() 的值.
的值.
【答案】(1)2![]() ,10
,10![]() ,2
,2![]() ;(2)S=
;(2)S=![]() ;(3)存在,x=5cm
;(3)存在,x=5cm
【解析】
(1)根据平移的距离分别求出AE、AD,再根据面积公式求出对应的答案即可;
(2)证明△BEF是等腰直角三角形,根据等腰直角三角形的性质求出AD、BE,过点C作CH⊥AB,利用面积相减的关系求出函数解析式;
(3)由(1)确定x>4cm,代入(2)的函数解析式求出方程解即可得到答案.
(1)∵△ABC是等腰直角三角形,
∴∠CAB=45°,
∵∠DEF=90°,
∴△AEF是等腰直角三角形,
∴AE=EF,
同理:△ADG是等腰直角三角形,
∴AD=DG,
当x=0cm时,AE=EF=2cm,∴S=![]()
![]() ;
;
当![]() 时,AD=DG=4cm,AE=EF=4+2=6cm,∴S=
时,AD=DG=4cm,AE=EF=4+2=6cm,∴S=![]() ;
;
当x=10cm时,AD=DG=10cm,AE=10+2=12cm,此时点E与点B重合,
∴S=![]()
![]() ;
;
故答案为:2![]() ,10
,10![]() ,2
,2![]() ;
;
(2)∵AD=DG=xcm,DE=2cm,
∴AE=(x+2)cm,
∴BE=(12-x-2)cm=(10-x)cm,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵∠BEF=90°,
∴∠BFE=∠B=45°,
∴△BEF是等腰直角三角形,
∴EF=BE=(10-x)cm,
过点C作CH⊥AB,
∴CH=![]() AB=6cm,
AB=6cm,
∴![]()
=![]() ,
,
=![]() ;
;
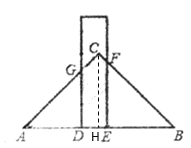
(3)存在,
由(1)知:当![]() 时S=10
时S=10![]() ,
,
∴当S=11![]() 时,x>4cm,
时,x>4cm,
∴![]() =11,
=11,
解得![]() ,
,
∴当x=5cm时,重叠部分面积为![]() .
.

 同步轻松练习系列答案
同步轻松练习系列答案【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
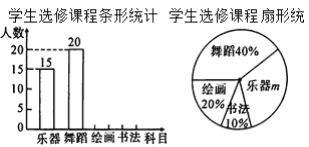
【题目】书籍是人类进步的阶梯.联合国教科文组织把每年的4月23日确定为“世界读书日”.某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数(名) | 43 | 31 | 15 | 5 | 4 | 2 |
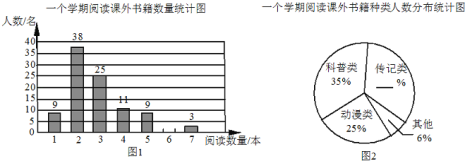
请你根据以上信息解答下列问题:
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有4000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.