题目内容
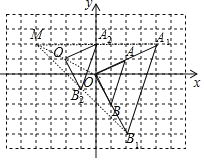
【题目】如图11,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2),P(a,b)是△OAB的边AB上一点.
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、P的对应点A1、P1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、P的对应点A2、P2的坐标;
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图11中标出位似中心M,并写出点M的坐标.

【答案】(1)A1(4,2),P1(2a,2b) (2)A2(0,2),P2(a-2,b+1)(3)△OA1B1与△O2A2B2是关于点M(-4,2)为位似中心的位似图形
【解析】试题分析: (1)分别延长![]() 使
使![]() 则
则
![]() 满足条件,然后写出点
满足条件,然后写出点![]() 的坐标;
的坐标;
(2)利用点平移的坐标规律写出![]() 的坐标,然后描点即可;
的坐标,然后描点即可;
(3)延长![]() 它们相交于一点,则可判定
它们相交于一点,则可判定![]() 和
和![]() 是位似图形,然后写交点坐标.
是位似图形,然后写交点坐标.
试题解析:如图, ![]() 为所作,点
为所作,点![]() 的坐标分别为
的坐标分别为![]()
(2)如图, ![]() 为所作,点
为所作,点![]() 的坐标分别为
的坐标分别为![]()
(3)如图: ![]() 和
和![]() 是位似图形,,如图,点M为所,位似中心M的坐标为
是位似图形,,如图,点M为所,位似中心M的坐标为![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目








