Question

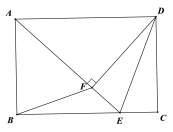
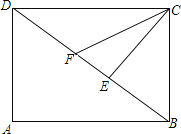
【题目】如图，矩形ABCD中，CE⊥BD于E，CF平分∠DCE与DB交于点F．

（1）求证：BF＝BC；

（2）若AB＝4cm，AD＝3cm，求CF的长．

Answer 1

【答案】（1）见解析；（2）CF＝cm．

【解析】

（1）要求证BF＝BC只要证明∠CFB＝∠FCB就可以，从而转化为证明∠BCE＝∠BDC就可以；

（2）已知AB＝4cm，AD＝3cm，就是已知BC＝BF＝3cm，CD＝4cm，在直角△BCD中，根据三角形的面积等于BDCE＝BCDC，就可以求出CE的长．要求CF的长，可以在直角△CEF中用勾股定理求得．其中EF＝BF﹣BE，BE在直角△BCE中根据勾股定理就可以求出，由此解决问题．

证明：（1）∵四边形ABCD是矩形，

∴∠BCD＝90°，

∴∠CDB+∠DBC＝90°．

∵CE⊥BD，

∴∠DBC+∠ECB＝90°．

∴∠ECB＝∠CDB．

∵∠CFB＝∠CDB+∠DCF，∠BCF＝∠ECB+∠ECF，∠DCF＝∠ECF，

∴∠CFB＝∠BCF

∴BF＝BC

（2）∵四边形ABCD是矩形，

∴DC＝AB＝4（cm），BC＝AD＝3（cm）．

在Rt△BCD中，由勾股定理得BD＝＝5．

又∵BDCE＝BCDC，

∴CE＝．

∴BE＝．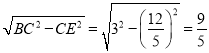

∴EF＝BF﹣BE＝3﹣．

∴CF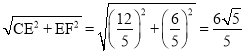＝cm．