题目内容
如图,已知动点A在函数 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .

试题分析:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t,
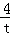 ),则AD=AB=DG=
),则AD=AB=DG=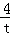 ,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=
,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积= t2+
t2+ ×
×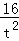 ,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=
,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE= ,再由△EFQ∽△DAE,求出QE=
,再由△EFQ∽△DAE,求出QE= ,△ADE∽△GPD,求出DP=:
,△ADE∽△GPD,求出DP=: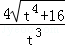 ,然后根据QE:DP=4:9,即可得出t2=
,然后根据QE:DP=4:9,即可得出t2= .
.解:解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
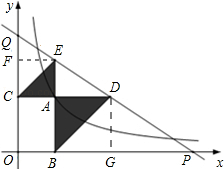
令A(t,
 ),则AD=AB=DG=
),则AD=AB=DG= ,AE=AC=EF=t.
,AE=AC=EF=t.在直角△ADE中,由勾股定理,得DE=
 =
= .
.∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE=
 ,
,∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP=
 .
.又∵QE:DP=4:9,
∴=
 :
: =4:9,
=4:9,解得t2=
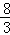 .
.∴图中阴影部分的面积=
 AC2+
AC2+ AB2=
AB2= t2+
t2+ ×
× =
=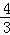 +3=
+3= .
.解法二:∵QE:DP=4:9,
设QE=4m,则DP=9m,
设FE=4t,则GP=9t,
∴A(4t,
 ),
),由AC="AE" AD=AB,
∴AE=4t,AD=
 ,DG=
,DG= ,GP="9t"
,GP="9t" ∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t:
 =
= :9t,即t2=
:9t,即t2= ,
,图中阴影部分的面积=
 4t×4t+
4t×4t+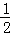 ×
× ×
× =
= .
.故答案为:
 .
.点评:本题考查了反比例函数的性质,勾股定理,相似三角形的判定与性质,三角形的面积等知识,综合性较强,有一定难度.根据QE:DP=4:9,得出t2的值是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
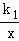 (x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
(x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
 x﹣1与反比例函数
x﹣1与反比例函数 (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )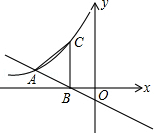
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+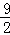 与双曲线y=
与双曲线y=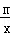 (m>0)的交点.
(m>0)的交点.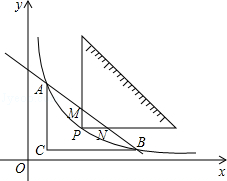
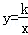 (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
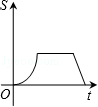 B.
B. C.
C.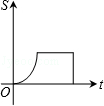 D.
D.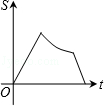
 )
)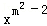 是反比例函数,且图象在第一,三象限,那么m的值是( )
是反比例函数,且图象在第一,三象限,那么m的值是( )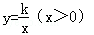 恰好经过点E,AB=4,AD=2,则K的值是 .
恰好经过点E,AB=4,AD=2,则K的值是 .
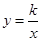 (k>0)与一次函数
(k>0)与一次函数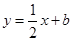 (b>0)的图像相交于两点
(b>0)的图像相交于两点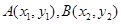 ,线段AB交y轴于点C,当
,线段AB交y轴于点C,当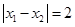 且AC=2BC时,k、b的值分别为( ).
且AC=2BC时,k、b的值分别为( ).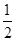 ,b=2
,b=2 ,b=1
,b=1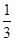 ,b=
,b=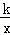 交矩形OABC的边分别于点D、E,若BD=2AD,且四边形ODBE的面积为8,则k= ______ .
交矩形OABC的边分别于点D、E,若BD=2AD,且四边形ODBE的面积为8,则k= ______ .