题目内容
如图,将一块直角三角形纸板的直角顶点放在C(1, )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+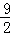 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.

(1)求m和k的值;
(2)设双曲线y= (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+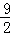 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.
(1)求m和k的值;
(2)设双曲线y=
 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.(1)k=﹣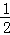 且m=4 (2)不存在,理由见解析
且m=4 (2)不存在,理由见解析
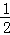 且m=4 (2)不存在,理由见解析
且m=4 (2)不存在,理由见解析试题分析:(1)由题意易知点A横坐标为1,代入Y=
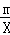 ,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组
,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组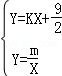 即可求m和k的值;
即可求m和k的值;(2)用反证法证明.假设存在,运用一元二次方程判别式即可解出.
解:(1)∵A,B在双曲线y=
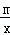 (m>0)上,AC∥y轴,BC∥x轴,
(m>0)上,AC∥y轴,BC∥x轴,∴A,B的坐标分别(1,m),(2m,
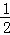 ).(1分)
).(1分)又点A,B在直线y=kx+
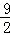 上,
上,∴
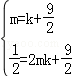 (2分)
(2分)解得
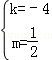 或
或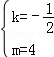 (4分)
(4分)当k=﹣4且m=
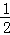 时,点A,B的坐标都是(1,
时,点A,B的坐标都是(1,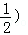 ,不合题意,应舍去;
,不合题意,应舍去;当k=﹣
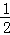 且m=4时,点A,B的坐标分别为(1,4),(8,
且m=4时,点A,B的坐标分别为(1,4),(8,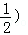 ,符合题意.
,符合题意.∴k=﹣
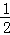
且m=4.(5分)
(2)假设存在点P使得MN=
 AB.
AB.∵AC∥y轴,MP∥y轴,
∴AC∥MP,
∴∠PMN=∠CAB,
∴Rt△ACB∽Rt△MPN,
∴
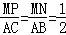 ,(7分)
,(7分)设点P坐标为P(x,
 )(1<x<8),
)(1<x<8),∴M点坐标为M(x,﹣
 x+
x+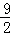 ),
),∴MP=﹣
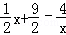 .
.又∵AC=4﹣
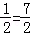 ,
,∴
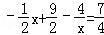 ,即2x2﹣11x+16=0(※)(9分)
,即2x2﹣11x+16=0(※)(9分)∵△=(﹣11)2﹣4×2×16=﹣7<0.
∴方程(※)无实数根.
∴不存在点P使得MN=
 AB.(10分)
AB.(10分)点评:此题难度中等,考查反比例函数的性质及坐标意义.解答此题时同学们要注意运用数形结合的思想.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 在每个象限中
在每个象限中 都随着
都随着 增大而减小,则
增大而减小,则 的值可以是 。(仅写一个)
的值可以是 。(仅写一个) ,x与y的对应值如下表:
,x与y的对应值如下表: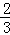 1 2 ﹣2 ﹣1 ﹣
1 2 ﹣2 ﹣1 ﹣ (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )

 上,点B在双曲线y=
上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )