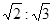题目内容
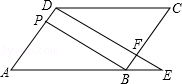
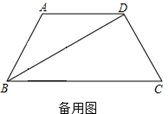
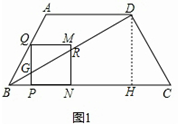
如图1,梯形 中,
中, ∥
∥ ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段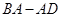 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点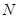 在射线
在射线 上,当
上,当 点到达
点到达 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒(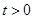 ).
).
(1)当正方形 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设正方形 与△
与△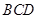 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
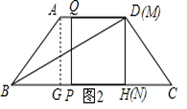
(3)如图2,当点 在线段
在线段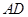 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△ 沿
沿 翻折,得到△
翻折,得到△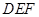 ,连接
,连接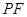 .是否存在这样的
.是否存在这样的 ,使△
,使△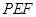 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

 中,
中,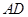 ∥
∥ ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒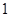 个单位长度的速度沿线段
个单位长度的速度沿线段 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段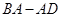 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点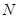 在射线
在射线 上,当
上,当 点到达
点到达 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒(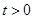 ).
).(1)当正方形
 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值;(2)在整个运动过程中,设正方形
 与△
与△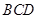 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;(3)如图2,当点
 在线段
在线段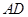 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△ 沿
沿 翻折,得到△
翻折,得到△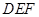 ,连接
,连接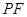 .是否存在这样的
.是否存在这样的 ,使△
,使△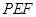 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

(1)当t=4时,正方形PQMN的边MN恰好过点D
(2)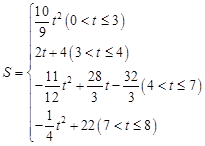
(3)当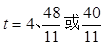 时,∆PEF是等腰三角形
时,∆PEF是等腰三角形
(2)
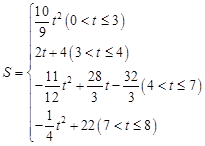
(3)当
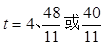 时,∆PEF是等腰三角形
时,∆PEF是等腰三角形试题分析:(1)作AG⊥BC,DH⊥BC,垂足分别为G、H,可以得出四边形AGHD为矩形,根据矩形的性质及相关条件可以得出△ABG≌△DCH,可以求出BG=CH的值,再由勾股定理就可以求出AG=DH的值,就可以求出BP的值,即可以求出结论t的值;
(2)运用求分段函数的方法,分四种情况,当0<t≤3,当3<t≤4,4<t≤7,7<t≤8时,运用梯形的面积公式和三角形的面积公式就可以求出S的值;
(3)先由条件可以求出EF=EQ=PQ-EP=4-
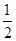 t,分为三种情况:EF=EP时可以求出t值,当FE=FP时,作FR⊥EP,垂足为R,可以求出t值,当PE=PF时,作PS⊥EF,垂足为S,可以求出t值.
t,分为三种情况:EF=EP时可以求出t值,当FE=FP时,作FR⊥EP,垂足为R,可以求出t值,当PE=PF时,作PS⊥EF,垂足为S,可以求出t值.试题解析:(1)如图2,作AG⊥BC于G,DH⊥BC于H,则四边形AGHD是矩形。
∵梯形ABCD中,AB=AD=DC=5,
∴∆ABG≌∆DCH,
∴
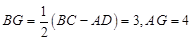 ,
,∴当正方形PQMN的边MN恰好过点D时,点M与点D重合,此时MQ=4,
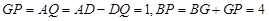 ,
,∴当t=4时,正方形PQMN的边MN恰好过点D。
(2)
如图1,当0<t≤3时,BP=t,∵
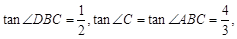
∴
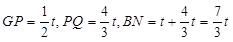 ,
,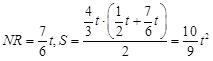
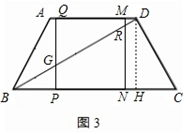
如图3,当3<t≤4时,BP="t,"
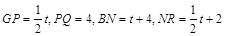
∴
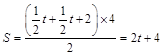
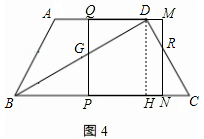
如图4,当4<t≤7时,BP="t,"
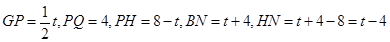
∴
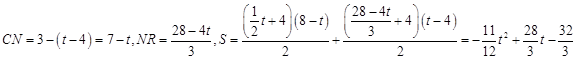
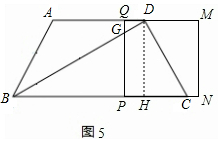
如图5,当7<t≤8时,BP="t,"
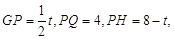
∴
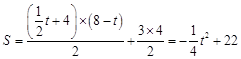
∴
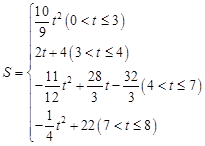
(3)∵
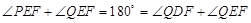 ,
,∴
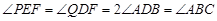
∴
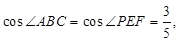
由(1)可知
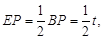 则
则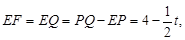
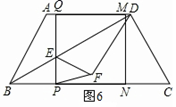
如图6,当EF=EP时,
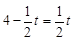
∴

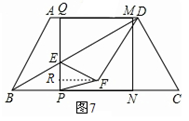
如图7,当FE=FP时,作FR⊥EP于R,∴
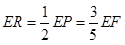
∴
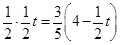
∴
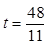
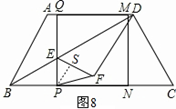
如图8,当PE=PF时,作PS⊥EF于S,∴
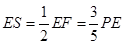
∴
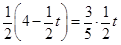
∴
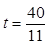
∴当
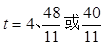 时,∆PEF是等腰三角形。
时,∆PEF是等腰三角形。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
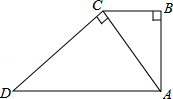
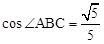 时,求AF及BE的长.
时,求AF及BE的长.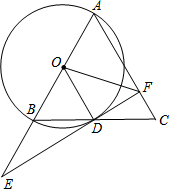
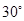 ,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;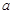 ,请直接写出每种拼法中最大三角形的斜边长.
,请直接写出每种拼法中最大三角形的斜边长.