题目内容
如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有 个.


3
设AP为x,表示出PB=10﹣x,然后分AD和PB是对应边,AD和BC是对应边两种情况,利用相似三角形对应边成比例列式求解即可.
解:设AP为x,
∵AB=10,
∴PB=10﹣x,
①AD和PB是对应边时,
∵△APD与△BPC相似,
∴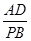 =
=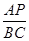 ,
,
即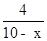 =
=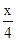 ,
,
整理得,x2﹣10x+16=0,
解得x1=2,x2=8,
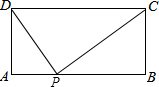
②AD和BC是对应边时,
∵△APD与△BPC相似,
∴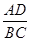 =
=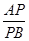 ,
,
即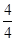 =
=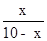 ,
,
解得x=5,
所以,当AP=2、5、8时,△APD与△BPC相似,
满足条件的点P有3个.
故答案为:3.
解:设AP为x,
∵AB=10,
∴PB=10﹣x,
①AD和PB是对应边时,
∵△APD与△BPC相似,
∴
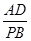 =
=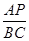 ,
,即
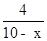 =
=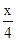 ,
,整理得,x2﹣10x+16=0,
解得x1=2,x2=8,
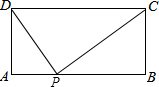
②AD和BC是对应边时,
∵△APD与△BPC相似,
∴
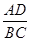 =
=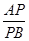 ,
,即
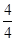 =
=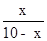 ,
,解得x=5,
所以,当AP=2、5、8时,△APD与△BPC相似,
满足条件的点P有3个.
故答案为:3.

练习册系列答案
相关题目
 中,
中,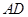 ∥
∥ ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒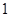 个单位长度的速度沿线段
个单位长度的速度沿线段 ,交折线段
,交折线段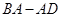 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点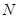 在射线
在射线 点时,运动结束.设点
点时,运动结束.设点 秒(
秒(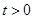 ).
). 恰好经过点
恰好经过点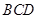 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 交于点
交于点 ,将△
,将△ 沿
沿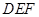 ,连接
,连接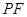 .是否存在这样的
.是否存在这样的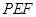 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的
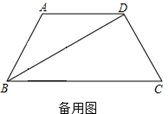
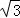 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
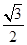 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;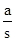 的值;
的值;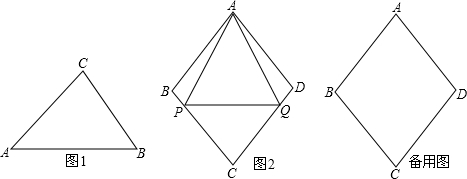



 ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )



