题目内容
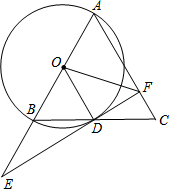
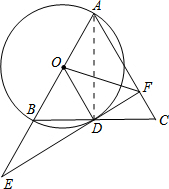
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
(1)求证:OD∥AC;
(2)当AB=10,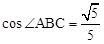 时,求AF及BE的长.
时,求AF及BE的长.
(1)求证:OD∥AC;
(2)当AB=10,
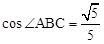 时,求AF及BE的长.
时,求AF及BE的长.
(1)证明见解析;(2)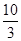 .
.
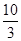 .
.试题分析:(1)若要证明OD∥AC,则可转化为证明∠C=∠ODB即可.
(2)连接AD,首先利用已知条件可求出BD的长,再证明△ADC∽△AFD,利用相似三角形的性质:对应边的比值相等即可求出AF及BE的长.
试题解析:(1)∵AB=AC,∴∠ABC=∠C.
∵OB=OD,∴∠OBD=∠ODB.∴∠C=∠ODB.
∴OD∥AC.
(2)如图,连接AD,
∵AB为直径,∴AB⊥BD.∴∠ADC=90°.
∵AB=10,
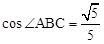 ,∴BD=AB•cos∠ABC=
,∴BD=AB•cos∠ABC=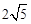 .∴AD=
.∴AD=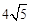 .
.∵DF是圆的切线,∴OD⊥DF.∴∠ODF=90°.
∵AC∥OD,∴∠AFD=90°.
∵∠ADC=∠AFD,∠DAF=∠CAD,∴△ADC∽△AFD,
∴
 ,即
,即 ,解得AF=8.
,解得AF=8.∵OD∥AF,∴
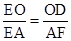 ,即
,即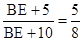 .
.∴BE=
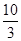 .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
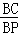 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;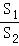 的值.
的值.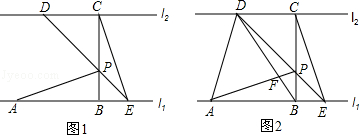
 中,
中,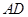 ∥
∥ ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒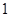 个单位长度的速度沿线段
个单位长度的速度沿线段 ,交折线段
,交折线段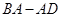 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点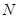 在射线
在射线 点时,运动结束.设点
点时,运动结束.设点 秒(
秒(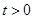 ).
). 恰好经过点
恰好经过点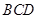 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 交于点
交于点 ,将△
,将△ 沿
沿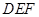 ,连接
,连接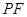 .是否存在这样的
.是否存在这样的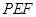 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的