��Ŀ����
����ѧ���ϣ�ͬѧ���о�ͼ�ε�ƴ�����⣮
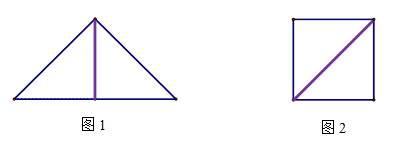
���磺����ȫ�ȵĵ���ֱ��������ֽƬ����ƴ��һ����ĵ���ֱ�������Σ���ͼ1����Ҳ��ƴ��һ�������Σ���ͼ2����
��1�������������Ƶ�ֱ��������ֽƬ������һ����Ϊ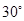 ��ǡ�ÿ���ƴ����һ������30��ǵ�ֱ�������Σ���ô��ԭ��������������ֽƬ�У��ϴ�����С��ֽƬ�����Ʊ�Ϊ________���뻭��ƴ�ӵ�ʾ��ͼ��
��ǡ�ÿ���ƴ����һ������30��ǵ�ֱ�������Σ���ô��ԭ��������������ֽƬ�У��ϴ�����С��ֽƬ�����Ʊ�Ϊ________���뻭��ƴ�ӵ�ʾ��ͼ��
��2������һ������ǡ������������һ����Ϊ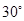 ��ֱ��������ֽƬƴ�ɣ����㻭�����ֲ�ͬƴ����ʾ��ͼ����ƴ��������ε��������У���ÿ��ƴ������С�������ε�б�߳�Ϊ
��ֱ��������ֽƬƴ�ɣ����㻭�����ֲ�ͬƴ����ʾ��ͼ����ƴ��������ε��������У���ÿ��ƴ������С�������ε�б�߳�Ϊ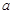 ����ֱ��д��ÿ��ƴ������������ε�б�߳���
����ֱ��д��ÿ��ƴ������������ε�б�߳���
���磺����ȫ�ȵĵ���ֱ��������ֽƬ����ƴ��һ����ĵ���ֱ�������Σ���ͼ1����Ҳ��ƴ��һ�������Σ���ͼ2����

��1�������������Ƶ�ֱ��������ֽƬ������һ����Ϊ
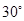 ��ǡ�ÿ���ƴ����һ������30��ǵ�ֱ�������Σ���ô��ԭ��������������ֽƬ�У��ϴ�����С��ֽƬ�����Ʊ�Ϊ________���뻭��ƴ�ӵ�ʾ��ͼ��
��ǡ�ÿ���ƴ����һ������30��ǵ�ֱ�������Σ���ô��ԭ��������������ֽƬ�У��ϴ�����С��ֽƬ�����Ʊ�Ϊ________���뻭��ƴ�ӵ�ʾ��ͼ����2������һ������ǡ������������һ����Ϊ
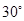 ��ֱ��������ֽƬƴ�ɣ����㻭�����ֲ�ͬƴ����ʾ��ͼ����ƴ��������ε��������У���ÿ��ƴ������С�������ε�б�߳�Ϊ
��ֱ��������ֽƬƴ�ɣ����㻭�����ֲ�ͬƴ����ʾ��ͼ����ƴ��������ε��������У���ÿ��ƴ������С�������ε�б�߳�Ϊ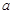 ����ֱ��д��ÿ��ƴ������������ε�б�߳���
����ֱ��д��ÿ��ƴ������������ε�б�߳�����1��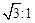 ��ƴͼ����������2��ƴͼ����������������ε�б�߳��ֱ���
��ƴͼ����������2��ƴͼ����������������ε�б�߳��ֱ���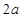 ,
,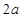 ��
��
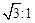 ��ƴͼ����������2��ƴͼ����������������ε�б�߳��ֱ���
��ƴͼ����������2��ƴͼ����������������ε�б�߳��ֱ���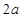 ,
,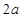 ��
�������������1���������������κͺ�30��ֱ�������ε����ʿɵ�.
��2���������������κ;��ε����ʿɵ�.
�����������1��
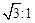 ��ƴͼ���£�
��ƴͼ���£�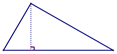
��2��ƴͼ���£�


��������ε�б�߳��ֱ���
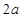 ,
,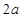 ��
��
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 �У�
��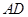 ��
�� ��
�� ��
�� ��һ������
��һ������ �ӵ�
�ӵ� ��������ÿ��
��������ÿ��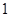 ����λ���ȵ��ٶ����߶�
����λ���ȵ��ٶ����߶� �������߶�
�������߶�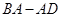 �ڵ�
�ڵ� ����
���� ��������������
�������������� ����
����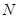 ������
������ ��ʱ���˶����������
��ʱ���˶���������� �루
�루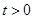 ����
���� ǡ�þ�����
ǡ�þ�����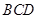 ���غϲ������Ϊ
���غϲ������Ϊ ����ֱ��д��
����ֱ��д�� ���ڵ�
���ڵ� ������
������ ��
��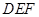 ������
������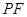 ���Ƿ����������
���Ƿ����������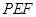 �ǵ��������Σ������ڣ������Ӧ��
�ǵ��������Σ������ڣ������Ӧ��
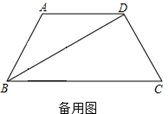
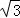 ��AF=4
��AF=4 ����AE�ij���
����AE�ij���
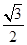 ����֤����ABC�ǡ����������Ρ���
����֤����ABC�ǡ����������Ρ���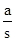 ��ֵ��
��ֵ��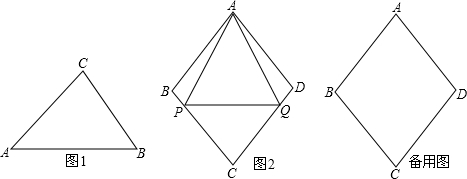

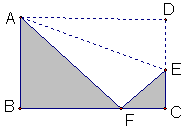

 ������A�������Ϊ(1��2)����������A��B��C��D����������ABCD�����Ʊ���(����)
������A�������Ϊ(1��2)����������A��B��C��D����������ABCD�����Ʊ���(����)



