题目内容
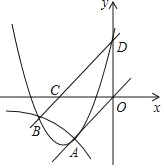
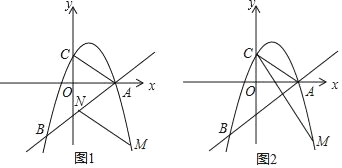
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3与直线y=x﹣3交于点A(3,0)和点B(﹣2,n),与y轴交于点C.
(1)求出抛物线的函数表达式;
(2)在图1中,平移线段AC,点A、C的对应点分别为M、N,当N点落在线段AB上时,M点也恰好在抛物线上,求此时点M的坐标;
(3)如图2,在(2)的条件下,在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)M点坐标为(4,﹣2);(3)P点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先利用直线解析式确定B(﹣2,﹣5),然后利用待定系数法求抛物线解析式;
(2)解方程组﹣x2+2x+3=0得A(3,0),易得C(0,3),设N(t,t﹣3),利用点利用的规律当点N先向下平移3个单位,再向右平移3个单位得到点M,则M(t+3,t﹣6),把M(t+3,t﹣6)代入y=﹣x2+2x+3得t﹣6=﹣(t+3)2+2(t+3)+3,当点N先向上平移3个单位,再向左平移3个单位得到点M,则M(t﹣3,t),把M(t﹣3,t)代入y=﹣x2+2x+3得t=﹣(t﹣3)2+2(t﹣3)+3,然后解方程求出t得到满足条件的M点坐标;
(3)利用待定系数法求出直线MC的解析式为y=﹣![]() x+3,利用AP∥MC可设AP的解析式为y=﹣
x+3,利用AP∥MC可设AP的解析式为y=﹣![]() x+p,则AP的解析式为y=﹣
x+p,则AP的解析式为y=﹣![]() x+
x+![]() ,通过解方程组
,通过解方程组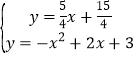 得此时P点坐标;再利用平移的方法得到再直线CM下方得到直线y=﹣
得此时P点坐标;再利用平移的方法得到再直线CM下方得到直线y=﹣![]() x+
x+![]() 到直线CM的距离等于直线y=﹣
到直线CM的距离等于直线y=﹣![]() x+
x+![]() 到直线CM的距离相等,然后解方程
到直线CM的距离相等,然后解方程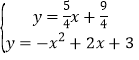 得此时P点坐标.
得此时P点坐标.
(1)把(﹣2,n)代入y=x﹣3得n=﹣2﹣3=﹣5,则B(﹣2,﹣5),
把A(3,0),B(﹣2,﹣5)代入得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(3,0),
当x=0时,y=﹣x2+2x+3=3,则C(0,3)
设N(t,t﹣3),
∵AC平移得到MN,
∴AC∥MN,AC=MN,
而点C先向下平移3个单位,再向右平移3个单位得到点A,
当点N先向下平移3个单位,再向右平移3个单位得到点M,则M(t+3,t﹣6),
把M(t+3,t﹣6)代入y=﹣x2+2x+3得t﹣6=﹣(t+3)2+2(t+3)+3,解得t1=1,t2=﹣6,
∴M点的坐标为(4,﹣5),(﹣3,﹣12)(舍去)
当点N先向上平移3个单位,再向左平移3个单位得到点M,则M(t﹣3,t),
把M(t﹣3,t)代入y=﹣x2+2x+3得t=﹣(t﹣3)2+2(t﹣3)+3,解得t1=3(舍去),t2=4,
∴M点的坐标为(﹣1,4)(舍去),
综上所述,M点坐标为(4,﹣2);
(3)设直线CM的解析式为y=mx+n,
把C(0,3),M(4,﹣2)代入得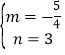 ,
,
∴直线MC的解析式为y=﹣![]() x+3,
x+3,
∵△PMC的面积与△AMC的面积相等,
∴AP∥MC,
设AP的解析式为y=﹣![]() x+p,
x+p,
把A(3,0)代入得p=![]() ,
,
∴AP的解析式为y=﹣![]() x+
x+![]() ,
,
解方程组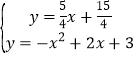 得
得![]() 或
或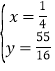 ,此时P点坐标为(
,此时P点坐标为(![]() ,
,![]() );
);
直线AP的解析式为y=﹣![]() x+
x+![]() 与y轴的交点坐标为(0,
与y轴的交点坐标为(0,![]() ),
),
∵![]() ﹣3=
﹣3=![]() ,
,
把直线CM向下平移![]() 个单位得到y=﹣
个单位得到y=﹣![]() x+
x+![]() ,
,
解方程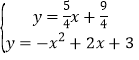 得
得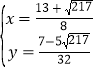 或
或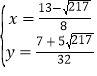 ,此时P点坐标为(
,此时P点坐标为(![]() ),(
),(![]() ),
),
综上所述,P点坐标为(![]() ,
,![]() )或(
)或(![]() )或(
)或(![]() ).
).