题目内容
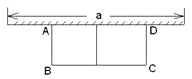
【题目】如图是某地区一条公路隧道入口在平面直角坐标系中的示意图,点A和A1、点B和B1分别关于y轴对称.隧道拱部分BCB1为一段抛物线,最高点C离路面AA1的距离为8 m,点B离路面AA1的距离为6 m,隧道宽AA1为16 m.
(1)求隧道拱部分BCB1对应的函数表达式.
(2)现有一大型货车,装载某大型设备后,宽为4 m,装载设备的顶部离路面均为7 m,问:它能否安全通过这个隧道?并说明理由.

【答案】(1)y=-![]() x2+8(-8≤x≤8);(2)该货车能安全通过这个隧道.理由见解析.
x2+8(-8≤x≤8);(2)该货车能安全通过这个隧道.理由见解析.
【解析】
(1)求出B,C的坐标,待定系数法即可解题;(2)利用货车的宽度求出此时允许通过的最大高度进行比较即可解题.
(1)由已知得OA=OA1=8 m,OC=8 m,AB=6 m.故C(0,8),B(-8,6).设抛物线BCB1对应的函数表达式为y=ax2+8,将B点坐标代入,得a·(-8)2+8=6,解得a=-![]() ,所以y=-
,所以y=-![]() x2+8(-8≤x≤8).
x2+8(-8≤x≤8).
(2)能.若货车从隧道正中行驶,则其最右边到y轴的距离为2 m.
如图,设抛物线上横坐标为2的点为点D,过点D作DE⊥AA1于点E.
当x=2时,y=-![]() ×22+8=
×22+8=![]() ,即D(2,
,即D(2,![]() ),所以DE=
),所以DE=![]() m.
m.
因为![]() >7,所以该货车能安全通过这个隧道.
>7,所以该货车能安全通过这个隧道.

练习册系列答案
相关题目