题目内容
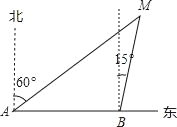
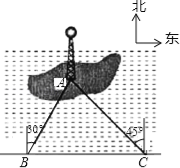
【题目】如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再次测得A在C的北偏西45°的方向上（其中A、B、C在同一平面上）．求这个标志性建筑物底部A到岸边BC的最短距离．
【答案】这个标志性建筑物底部A到岸边BC的最短距离为（6﹣2
）公里
【解析】
试题要求这个标志性建筑物底部A到岸边BC的最短距离也就是要求出点A到直线BC的最短距离，过点A作AD⊥BC于D，然后利用所给条件求出AD的长即可
试题解析：过A作AD⊥BC于D，则AD的长度就是A到岸边BC的最短距离．
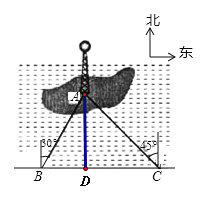
在Rt△ACD中，∠ACD=45°，设AD=x，则CD=AD=x，
在Rt△ABD中，∠ABD=60°，
由tan∠ABD=
，即tan60°=
，
所以BD=
=
x，
又BC=4，即BD+CD=4，所以x+x=4，
解得x=6﹣2
．
答：这个标志性建筑物底部A到岸边BC的最短距离为（6﹣2）公里．
练习册系列答案
相关题目
