��Ŀ����
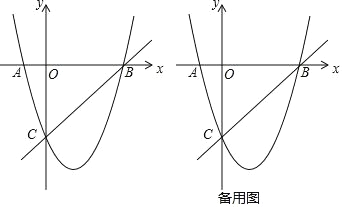
����Ŀ����ƽ��ֱ������ϵ�У����κ�����ͼ���������� A����1��0����B��4��0����C
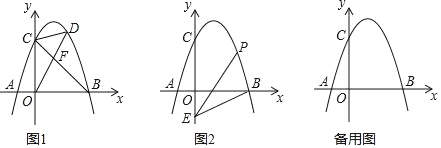
��0����4�����㣬�� P ��ֱ�� BC �·���������һ���㣮
��1�� ��������κ����Ľ���ʽ��
��2�� �Ƿ���ڵ� P��ʹ��POC ���� OC Ϊ�ױߵĵ��������Σ������ڣ���� P �����ꣻ�������ڣ���˵�����ɣ�
��3�� �����������Ƿ���ڵ� D����� A ���غϣ�ʹ�� S��DBC��S��ABC�������ڣ������ D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)�����߽���ʽΪy��x2��3x��4��(2)��������������P�㣬������Ϊ��![]() ����2����(3)��������������D�㣬������Ϊ��5��6����
����2����(3)��������������D�㣬������Ϊ��5��6����
��������
��1����A��B��C��������꣬���ô���ϵ��������������߽���ʽ��
��2���������֪��P���߶�OC�Ĵ�ֱƽ�����ϣ�������P�������꣬���������߽���ʽ�����P�����ꣻ
��3�����ڣ�������������ۣ������ô���ϵ�����Լ��ⷽ���鼴�ɽ�����⣮
(1)�������߽���ʽΪy��ax2+bx+c��
��A��B��C�����������ɵ�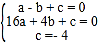 �����
����� ��
��
�������߽���ʽΪy��x2��3x��4��
(2)��ͼ1����OC�Ĵ�ֱƽ����DP����OC�ڵ�D����BC�·��������ڵ�P��
��PO��PC����ʱP�㼴Ϊ���������ĵ㣬
��C��0����4����
��D��0����2����
��P����������2��
���������߽���ʽ�ɵ�x2��3x��4����2�����x��![]() ��С��0����ȥ����x��
��С��0����ȥ����x��![]() ��
��
���������������P�㣬������Ϊ��![]() ����2����
����2����
(3)��ͼ2��
�ٵ�D����ֱ��BC���Ϸ�ʱ����A����AD1��BC������������D1����ʱ��ʹ��S��DBC��S��ABC��
��B��4��0����C��0����4����
��ֱ��BC�Ľ���ʽΪy��x��4��
��AD1��BC��
����ֱ��AD11�Ľ���ʽΪy��x+n��
��A����1��0������ã�0����1+n����n��1��
��ֱ��AD1�Ľ���ʽΪy��x+1��
��![]() ��
��![]() ��
��![]() ��
��
��D1��������5��6����
�ڵ�D����ֱ��BC���·�ʱ��
��ֱ��AD1�Ľ���ʽΪy��x+1��ֱ֪��AD1��y��Ľ���E������Ϊ��0�� 1����
��CE��5��
��ֱ��AD�Ľ���ʽΪy��x��10��
�߷���x2��3x��4��x��10��ʵ������
�ʴ�������������D�㣬������Ϊ��5��6����