题目内容

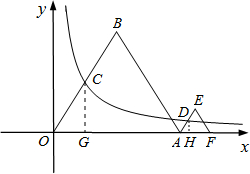
如图，等边△OAB和等边△AFE的一边都在x轴上，双曲线y=
k
x
（k＞0）经过边OB的中点C和AE的中点D．已知等边△OAB的边长为4．
（1）求该双曲线所表示的函数解析式；
（2）求等边△AEF的边长．
（1）过点C作CG⊥OA于点G，
∵点C是等边△OAB的边OB的中点，
∴OC=2，∠AOB=60°，
∴OG=1，CG=OG•tan60°=1•
3
=
3
，
∴点C的坐标是（1，
3
），
由
3
=
k
1
，得：k=
3
，
∴该双曲线所表示的函数解析式为y=
3
x
；

（2）过点D作DH⊥AF于点H，设AH=a，则DH=
3
a．
∴点D的坐标为（4+a，
3
a），
∵点D是双曲线y=
3
x
上的点，
由xy=
3
，得
3
a（4+a）=
3
，
即：a2+4a-1=0，
解得：a1=
5
-2，a2=-
5
-2（舍去），
∴AD=2AH=2
5
-4，
∴等边△AEF的边长是2AD=4
5
-8．
练习册系列答案
相关题目
如图，在平面直角坐标系中，直线y=-2x+2与x轴、y轴分别相交于点A，B，四边形ABCD是正方形，反比例函数y=
k
x
在第一象限的图象经过点D．
（1）求D点的坐标，以及反比例函数的解析式；
（2）若K是双曲线上第一象限内的任意点，连接AK、BK，设四边形AOBK的面积为S；试推断当S达到最大值或最小值时，相应的K点横坐标；并直接写出S的取值范围．
（3）试探究：将正方形ABCD沿左右（或上下）一次平移若干个单位后，点C的对应点恰好落在双曲线上的方法．
已知反比例函数y=
k
x
的图象经过点A（-
3
，1）．
（1）试确定此反比例函数的解析式；
（2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB．判断点B是否在此反比例函数的图象上，并说明理由；
（3）已知点P（m，
3
m+6）也在此反比例函数的图象上（其中m＜0），过P点作x轴的垂线，交x轴于点M．若线段PM上存在一点Q，使得△OQM的面积是
1
2
，设Q点的纵坐标为n，求n2-2
3
n+9的值．
如图，直线与y=2x双曲线y=
8
x
相交于点A、E，直线AB与双曲线交于点B，与x轴、y轴分别交于点C、D，且B点横坐标等于纵坐标的两倍，直线EB交x轴于点F，
（1）求直线AB的解析式；
（2）求证：△COD∽△CBF．
如图，已知反比例函数y=
k
x
的图象经过第二象限内的点A（-2，m），AB⊥x轴于B，△AOB的面积为3，
（1）求k，m的值；
（2）若直线y=ax+b经过点A，并且经过反比例函数y=
k
x
的图象上另一点C(n，-
3
2
)．
①求直线y=ax+b的解析式；
②设直线y=ax+b与x轴交于点M，求AM的长；
③根据图象写出使反比例函数y=
k
x
＞y=ax+b的值x的取值范围．
某蓄水池的排水管每小时排水8m3，6h可将满池水全部排空．
（1）蓄水池的容积是多少？
（2）如果增加排水管，使每小时的排水量达到Q（m3），那么将满池水排空所需的时间t（h）将如何变化？
（3）写出t与Q之间的关系式．
（4）如果准备在5h内将满池水排空，那么每小时的排水量至少为多少？
（5）已知排水管的最大排水量为每小时12m3，那么最少多长时间可将满池水全部排空？
已知：如图，O为平面直角坐标系的原点，半径为1的⊙B经过点O，且与x，y轴分交于点A，C，点A的坐标为（-
3
，0），AC的延长线与⊙B的切线OD交于点D．
（1）求OC的长和∠CAO的度数；
（2）求过D点的反比例函数的表达式．
用F牛顿的力作15焦耳的功，则力F与物体在力的作用下移动的距离s之间的函数关系的图象是（　　）
A．B．C．D．
小明家利用国家贷款100万元，购买了五脑山庄的一套住房，在交了首期付款后，每年需向银行付款y万元，预计x年后结清余款，y与x的函数关系如下图所示，试根据图象所提供的信息，回答下列问题：
（1）确定y与x之间的函数表达式，并说明小明家交了多少万元首付款；
（2）小明家若计划用15年时间结清余款，那么每年应向银行交付多万元？
（3）若打算每年付款不超过6万元，小明家至少要多少年才能结清余款？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网