题目内容
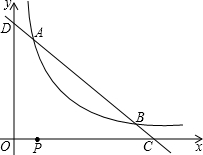
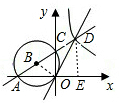
已知:如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x,y轴分交于点A,C,点A的坐标为(-
,0),AC的延长线与⊙B的切线OD交于点D.
(1)求OC的长和∠CAO的度数;
(2)求过D点的反比例函数的表达式.

| 3 |
(1)求OC的长和∠CAO的度数;
(2)求过D点的反比例函数的表达式.

(1)∵∠AOC=90°,
∴AC是⊙B的直径.
∴AC=2.
又∵点A的坐标为(-
,0),
∴OA=
.
∴OC=
=
=1.
∴sin∠CAO=
=
.
∴∠CAO=30°;
(2)如图,连接OB,过点D作DE⊥x轴于点E,
∵OD为⊙B的切线,
∴OB⊥OD.
∴∠BOD=90°.
∵AB=OB,
∴∠AOB=∠OAB=30°.
∴∠AOD=∠AOB+∠BOD=30°+90°=120°.
在△AOD中,∠ODA=180°-120°-30°=30°=∠OAD.
∴OD=OA=
.
在Rt△DOE中,∠DOE=180°-120°=60°,
∴OE=OD•cos60°=
OD=
,ED=OD•sin60°=
.
∴点D的坐标为(
,
).
设过D点的反比例函数的表达式为y=
,
∴k=
×
=
.
∴y=
.
∴AC是⊙B的直径.
∴AC=2.
又∵点A的坐标为(-
| 3 |
∴OA=
| 3 |
∴OC=
| AC2-OA2 |
22-(
|
∴sin∠CAO=
| OC |
| AC |
| 1 |
| 2 |
∴∠CAO=30°;
(2)如图,连接OB,过点D作DE⊥x轴于点E,
∵OD为⊙B的切线,
∴OB⊥OD.
∴∠BOD=90°.
∵AB=OB,
∴∠AOB=∠OAB=30°.
∴∠AOD=∠AOB+∠BOD=30°+90°=120°.
在△AOD中,∠ODA=180°-120°-30°=30°=∠OAD.
∴OD=OA=
| 3 |
在Rt△DOE中,∠DOE=180°-120°=60°,
∴OE=OD•cos60°=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴点D的坐标为(
| ||
| 2 |
| 3 |
| 2 |
设过D点的反比例函数的表达式为y=
| k |
| x |
∴k=
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 4 |
∴y=
3
| ||
| 4x |


练习册系列答案
相关题目
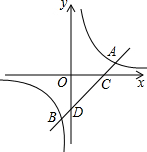 轴相交于C,D两点.
轴相交于C,D两点.