题目内容
【题目】阅读材料:
我们知道|x|=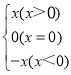 ,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值),在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值),在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1≤x<2时,原式=x+1-(x-2)=3;
(3)当x≥2时,原式=x+1+x-2=2x-1.综上所述,原式=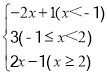
学以致用:
(Ⅰ)分别求出|x+3|和|x-1|的零点值;
(Ⅱ)化简代数式|x+3|+|x-1|;
拓展应用:
(Ⅲ)求函数y=|x+3|+|x-1|(-3≤x≤3)的最大值和最小值.
【答案】(1)零点值分别为-3和1;(2)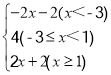 ;(3)最大值是8和最小值是4.
;(3)最大值是8和最小值是4.
【解析】
试题分析:(Ⅰ)阅读材料,根据零点值的求法,即绝对值里面的代数式等于0,即可解答;
(Ⅱ)根据阅读材料中,化简带绝对值的代数式的方法,根据x的取值范围,分为三种情况,根据绝对值的性质解答即可;
(Ⅲ)分x<-3、-3≤x≤1、x>1分别化简,结合x的取值范围确定代数式值的范围,从而求出函数的最值.
试题解析:(Ⅰ)令x+3=0和x-1=0,分别求得x=-3,x=1,
所以|x+3|和|x-1|的零点值分别为-3和1;
(Ⅱ)在实范围内,零点值x=-3和x=1可将全体实数分成不重复且不遗漏的如下3种情况:
(1)当x<-3时,原式=-(x+3)-(x-1)=-2x-2;
(2)当-3≤x<1时,原式=(x+3)-(x-1)=4;
(3)当x≥1时,原式=x+3+x-1=2x+2.
综上所述,原式=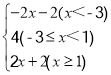 ;
;
(Ⅲ)由(Ⅱ)可化简函数为y=![]() .
.
该函数的大致图形如图所示:
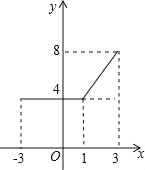
所以函数y=|x+3|+|x-1|(-3≤x≤3)的最大值是8和最小值是4.

【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请为两校设计一种省钱的购买服装方案.