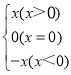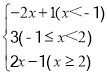Question

【题目】已知AC⊥BC于C，BC=a，CA=b，AB=c，下列选项中⊙O的半径为的是（ ）

Answer 1

【答案】C．

【解析】

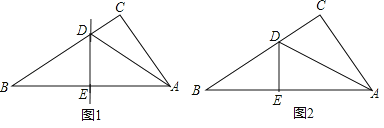
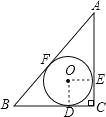
试题解析：A、设圆的半径是x，圆切AC于E，切BC于D，切AB于F，如图（1）同样得到正方形OECD，AE=AF，BD=BF，则a-x+b-x=c，求出x=，故本选项错误；

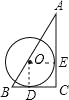
B、设圆切AB于F，圆的半径是y，连接OF，如图（2），

则△BCA∽△OFA，

∴，

∴，解得：y=，故本选项错误；

C、连接OE、OD，

∵AC、BC分别切圆O于E、D，

∴∠OEC=∠ODC=∠C=90°，

∵OE=OD，

∴四边形OECD是正方形，

∴OE=EC=CD=OD，

设圆O的半径是r，

∵OE∥BC，∴∠AOE=∠B，

∵∠AEO=∠ODB，

∴△ODB∽△AEO，

∴，

，

解得：r=，故本选项正确；

从上至下三个切点依次为D，E，F；并设圆的半径为x；

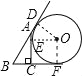
容易知道BD=BF，所以AD=BD-BA=BF-BA=a+x-c；

又∵b-x=AE=AD=a+x-c；所以x=，故本选项错误．

故选C．