Question

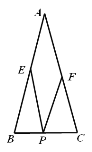
【题目】如图，四边形ABCD中，∠A=∠B=90°，P是线段AB上的一个动点．

（1）若AD=2，BC=6，AB=8，且以A，D，P为顶点的三角形与以B，C，P为顶点的三角形相似，求AP的长；

（2）若AD=a，BC=b，AB=m，则当a，b，m满足什么关系时，一定存在点P使△ADP∽△BPC？并说明理由．

Answer 1

【答案】（1）2或8；（2）m2﹣4ab≥0；理由见解析；

【解析】

(1)分和两种情形构建方程求解即可;

(2)由△ADP∽△BPC,可得=,即,整理得: x2﹣mx+ab=0,根据题意△≥0,即可解决问题;

（1）设AP=x．

∵以A，D，P为顶点的三角形与以B，C，P为顶点的三角形相似，

①当=时，=，解得x=2或8．

②当时，，解得x=2，

∴当A，D，P为顶点的三角形与以B，C，P为顶点的三角形相似，AP的值为2或8；

（2）设PA=x，

∵△ADP∽△BPC，

∴=，

∴=，

整理得：x2﹣mx+ab=0，

由题意△≥0，

∴m2﹣4ab≥0．

∴当a，b，m满足m2﹣4ab≥0时，一定存在点P使△ADP∽△BPC．