题目内容
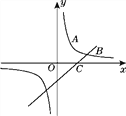
【题目】已知反比例函数y=![]() (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=-x+1的图象的一个交点的纵坐标是3,求m的值.
【答案】(1)m<5;(2)m=-1
【解析】试题分析:(1)由反比例函数y=![]() 的性质:当k<0时,在其图象的每个分支上,y随x的增大而增大,进而可得:m﹣5<0,从而求出m的取值范围;
的性质:当k<0时,在其图象的每个分支上,y随x的增大而增大,进而可得:m﹣5<0,从而求出m的取值范围;
(2)先将交点的纵坐标y=3代入一次函数y=﹣x+1中求出交点的横坐标,然后将交点的坐标代入反比例函数y=![]() 中,即可求出m的值.
中,即可求出m的值.
试题解析:解:(1)∵在反比例函数y=![]() 图象的每个分支上,y随x的增大而增大,
图象的每个分支上,y随x的增大而增大,
∴m﹣5<0,
解得:m<5;
(2)将y=3代入y=﹣x+1中,得:x=﹣2,
∴反比例函数y=![]() 图象与一次函数y=﹣x+1图象的交点坐标为:(﹣2,3).
图象与一次函数y=﹣x+1图象的交点坐标为:(﹣2,3).
将(﹣2,3)代入y=![]() 得:
得:
3=![]()
解得:m=﹣1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某景区在“春节”假期间,每天接待的游客人数统计如下:(单位:万人)
农历 | 十二月三十 | 正月初一 | 正月初二 | 正月初三 | 正月初四 | 正月初五 | 正月初六 |
人数 | 1.2 | 2.3 | 2 | 2.3 | 1.2 | 2.3 | 0.6 |
表中表示人数的一组数据中,众数和中位数分别是______和_______.