题目内容
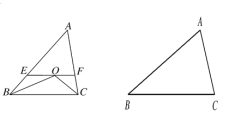
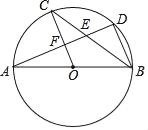
【题目】已知，△ABC中，∠A=68°，以AB为直径的⊙O与AC，BC的交点分别为D，E
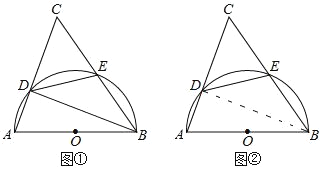
（Ⅰ）如图①，求∠CED的大小；
（Ⅱ）如图②，当DE=BE时，求∠C的大小．
【答案】（Ⅰ）68°（Ⅱ）56°
【解析】
（1）圆内接四边形的一个外角等于它的内对角,利用圆内接四边形的性质证明∠CED=∠A即可,（2）连接AE,在Rt△AEC中,先根据同圆中,相等的弦所对弧相等,再根据同圆中,相等的弧所对圆周角相等, 求出∠EAC,最后根据直径所对圆周是直角,利用直角三角形两锐角互余即可解决问题.
（Ⅰ）∵四边形ABED 圆内接四边形，
∴∠A+∠DEB=180°，
∵∠CED+∠DEB=180°，
∴∠CED=∠A，
∵∠A=68°，
∴∠CED=68°．
（Ⅱ）连接AE．
∵DE=BD，
∴
,
∴∠DAE=∠EAB=
∠CAB=34°，
∵AB是直径，
∴∠AEB=90°，
∴∠AEC=90°，
∴∠C=90°﹣∠DAE=90°﹣34°=56°
练习册系列答案
相关题目
