题目内容
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)求出点![]() ,点
,点![]() 的坐标.
的坐标.
(2)![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() 和
和![]() 的面积相等,求点
的面积相等,求点![]() 坐标.
坐标.
(3)如图2,平移直线![]() ,分别交
,分别交![]() 轴,
轴,![]() 轴于交于点
轴于交于点![]() ,
,![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,请直接写出所有符合条件的点
是等腰直角三角形?若存在,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
图1 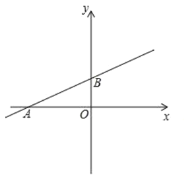 图2
图2 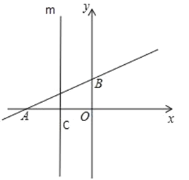
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]()
![]() .
.
【解析】
(1)根据A,B坐标的特点即可求解;
(2)分P点在线段AB上、直线AB上根据三角形的面积公式即可求解;
(3)设Q(-2,t),分别求出AB2,AQ2,BQ2,根据等腰三角形的性质分情况讨论即可求解.
(1)令y=![]() =0,解得x=-4,
=0,解得x=-4,
∴A(-4,0)
令x=0,y=![]() =2,
=2,
∴B(0,2)
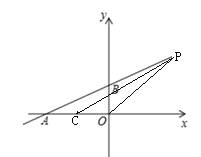
(2)如图,当P点在线段AB上,设P(x,![]() )
)
∵![]() ,A(-4,0),B(0,2)
,A(-4,0),B(0,2)
∴CO=2=OB,OA=4
∵![]() 和
和![]() 的面积相等
的面积相等
∴![]() BO×(-x)=
BO×(-x)= ![]() CO×(
CO×(![]() ),即
),即![]() ×2×(-x)=
×2×(-x)= ![]() ×2×(
×2×(![]() )
)
解得x=![]()
∴![]()
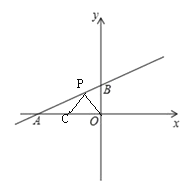
如图,当P点在直线AB上,当P在BA的延长线上,S△BOP>S△COP
故P在AB的延长线上,
设P(x,![]() )
)
∵![]() 和
和![]() 的面积相等
的面积相等
∴![]() BO×x=
BO×x= ![]() CO×(
CO×(![]() ),即
),即![]() ×2×x=
×2×x= ![]() ×2×(
×2×(![]() )
)
解得x=4
∴![]()
综上,![]() 或
或![]() ;
;
(3)∵过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,点
,点![]() 在直线
在直线![]() 上是
上是
∴设Q(-2,t),
∵A(-4,0),B(0,2)
∴AB2=20,AQ2=22+t2=4+t2,BQ2=22+(2-t)2=4+(2-t)2,
故当AB=BQ,即20=4+(2-t)2,
解得:t=-2或t=6
故Q![]()
故当AB=AQ,即20=4+t2,
解得:t=±4
故![]()
当AQ=BQ,即4+t2=4+(2-t)2,
解得:t=1
∵(-2,1)在直线y=![]() 上,故舍去
上,故舍去
∴Q点坐标为:![]()
![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
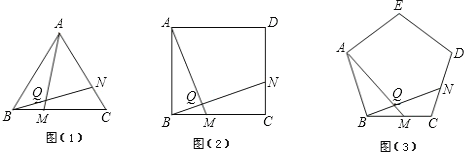
目标测试系列答案【题目】(1)如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形 | 正方形 | 正五边形 | …… | 正n边形 |
∠BQM的度数 |
|
| …… |
|