题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,相向而行,速度都为
同时出发,相向而行,速度都为![]() .以
.以![]() 为一边向上作正方形
为一边向上作正方形![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,单位:
,单位:![]() ,正方形
,正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() .
.
![]() 当
当![]() 时,点
时,点![]() 与点
与点![]() 重合.
重合.
![]() 当
当![]() 时,点
时,点![]() 在
在![]() 上.
上.
![]() 当点
当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,求
两点)时,求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.

【答案】(1)1;(2)![]() ;(3)当点
;(3)当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,
两点)时,![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为: .
.
【解析】
(1)当点P与点Q重合时,此时AP=BQ=t,且AP+BQ=AB=2,由此列一元一次方程求出t的值;
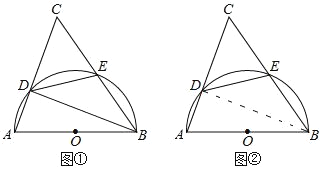
(2)当点D在QF上时,如图1所示,此时AP=BQ=t.由相似三角形比例线段关系可得PQ=![]() t,从而由关系式AP+PQ+BQ=AB=2,列一元一次方程求出t的值;
t,从而由关系式AP+PQ+BQ=AB=2,列一元一次方程求出t的值;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,运动过程可以划分为两个阶段:
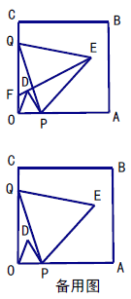
①当1<t≤![]() 时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S;
时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S;
②当![]() <t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“S=S正方形APDE﹣S△AQF﹣S△DMN”求出.
<t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“S=S正方形APDE﹣S△AQF﹣S△DMN”求出.
(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,∴t+t=2,解得:t=1s.
故答案:1.
(2)当点D在QF上时,如图1所示,此时AP=BQ=t.
∵QF∥BC,APDE为正方形,∴△PQD∽△ABC,∴DP:PQ=AC:AB=2,则PQ=![]() DP=
DP=![]() AP=
AP=![]() t.
t.
由AP+PQ+BQ=AB=2,得:t+![]() t+t=2,解得:t=
t+t=2,解得:t=![]() .
.
故答案:![]() .
.
(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP=![]() t,求得t=
t,求得t=![]() s,进一步分析可知此时点E与点F重合;
s,进一步分析可知此时点E与点F重合;
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
①当1<t≤![]() 时,如答图3所示,此时重合部分为梯形PDGQ.
时,如答图3所示,此时重合部分为梯形PDGQ.
此时AP=BQ=t,∴AQ=2﹣t,PQ=AP﹣AQ=2t﹣2;
易知△ABC∽△AQF,可得AF=2AQ,EF=2EG,∴EF=AF﹣AE=2(2﹣t)﹣t=4﹣3t,EG=![]() EF=2﹣
EF=2﹣![]() t,∴DG=DE﹣EG=t﹣(2﹣
t,∴DG=DE﹣EG=t﹣(2﹣![]() t)=
t)=![]() t﹣2.
t﹣2.
S=S梯形PDGQ=![]() (PQ+DG)PD=
(PQ+DG)PD=![]() [(2t﹣2)+(
[(2t﹣2)+(![]() t﹣2)]t=
t﹣2)]t=![]() t2﹣2t;
t2﹣2t;
②当![]() <t<2时,如答图4所示,此时重合部分为一个多边形.
<t<2时,如答图4所示,此时重合部分为一个多边形.
此时AP=BQ=t,∴AQ=PB=2﹣t,易知△ABC∽△AQF∽△PBM∽△DNM,可得AF=2AQ,PM=2
又∵DM=DP﹣PM=t﹣(4﹣2t)=3t﹣4,∴DN=![]() (3t﹣4)=
(3t﹣4)=![]() t﹣2,DM=3t﹣4.
t﹣2,DM=3t﹣4.
S=S正方形APDE﹣S△AQF﹣S△DMN=AP2﹣![]() AQAF﹣
AQAF﹣![]() DNDM
DNDM
=t2﹣![]() (2﹣t)(4﹣2t)﹣
(2﹣t)(4﹣2t)﹣![]() ×
×![]() (3t﹣4)×(3t﹣4)
(3t﹣4)×(3t﹣4)
=﹣![]() t2+10t﹣8.
t2+10t﹣8.
综上所述:当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:S= .
.

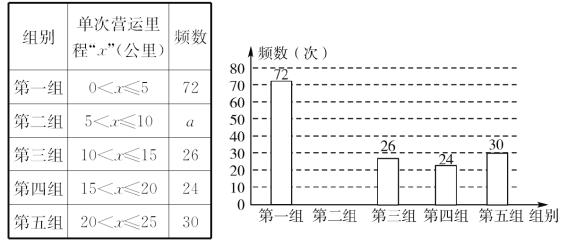
【题目】某校传统文化社团某天进行纳新活动,组织初一新生选报兴趣学社,由于当天报名人数较多,从现场随机抽查部分学生的报名意向进行统计,并绘制出不完全的频数分布表和频数分布直方图,如下所示:
传统文化 学社 | 报名频数 (人数) | 报名 频率 | 录取率 |
灯谜 | 12 |
|
|
书法 | 27 | 0.45 | 0.4 |
剪纸 |
| 0.3 |
|
南音 |
|
|
|
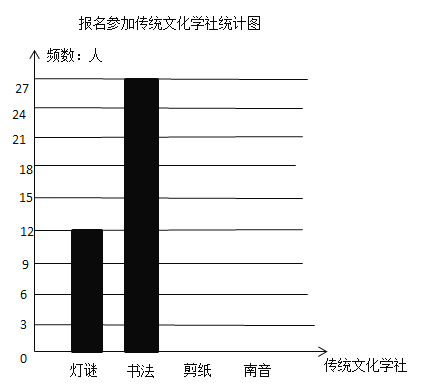
请根据上述图表,完成下列各题:
(1)填空:![]() ,
,![]() ,
,![]() ,现场共抽查了 名学生;
,现场共抽查了 名学生;
(2)请把条线统计图补充完整;
(3)现有1200个学生报名参加该校传统文化社团,则可以估计被剪纸学社录取的学生数比南音学社录取的学生数多了多少人?若把所有被录取人数按表中学社制作成扇形统计图,则被灯谜学社录取的学生数的扇形圆心角为多少度?