题目内容
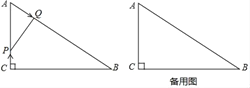
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= . 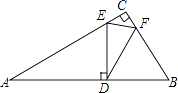
【答案】![]() 或
或 ![]()
【解析】解:∵∠EDF=30°,ED⊥AB于D,
∴∠FDB=∠B=60°,
∴△BDF是等边三角形;
∵BC=1,∴AB=2;
∵BD=BF,
∴2﹣AD=1﹣CF;
∴AD=CF+1.
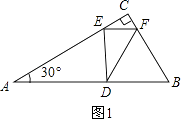
①如图1,∠FED=90°,△CEF∽△EDF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,CF= ![]() ;
;
∴AD= ![]() +1=
+1= ![]() ;
;
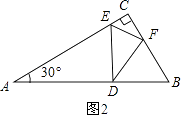
②如图2,∠EFD=90°,△CEF∽△FED,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ;
;
解得,CF= ![]() ;
;
∴AD= ![]() +1=
+1= ![]() .
.
故答案为 ![]() 或
或 ![]() .
.
由于∠EDF=30°,且DE总垂直于AB,因此∠FDB=60°,从而得出△FDB是等边三角形,故BD=BF,2-AD=1-CF,即AD=CF+1.由于∠C是直角,当△CEF∽△DEF时,△DEF必为直角三角形,那么可分两种情况讨论:①∠DEF=90°,此时,△CEF∽△DEF;②∠DFE=90°,此时△CEF∽△FED;可根据各相似三角形得到的比例线段求出CF的值,进而可求得AD的值.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
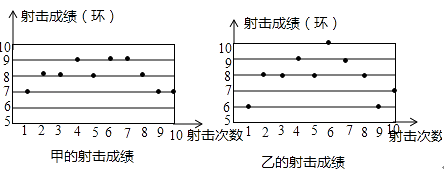
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁