题目内容

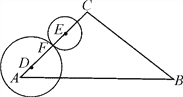
【题目】如图，在△ABC中，∠A=45°，AB=，AC=6，点D，E为边AC上的点，AD=1，CE=2，点F为线段DE上一点（不与D，E重合），分别以点D、E为圆心，DF、EF为半径作圆.若两圆与边AB，BC共有三个交点时，线段DF长度的取值范围是_______.

【答案】或

【解析】分析：过D作DG⊥AG，垂足为G，过E点作EH⊥AB于H，则可求出DG、EH的长，再根据两圆与边AB，BC共有三个交点即可求出线段DF长度的取值范围.

详解：过D作DG⊥AG，垂足为G，过E点作EH⊥AB于H，

∵AD=1，∠A=45°，

∴DG=ADsin45°=,

∵AE=6-2=4, ∠A=45°，

∴EH=AEsin45°=2.

由于两圆与边AB，BC共有三个交点.

故可得线段DF长度的取值范围为：或.

故答案为：或.

练习册系列答案
相关题目

【题目】如图，在数轴上有三个点A、B、C，请回答下列问题．

（1）A、B、C三点分别表示 、 、 ；

（2）将点B向左移动3个单位长度后，点B所表示的数是 ；

（3）将点A向右移动4个单位长度后，点A所表示的数是 .

【题目】如图，点D在BC上，DE⊥AB于点E，DF⊥BC交AC于点F，BD=CF，BE=CD．若∠AFD=145°，则∠EDF=_____________.

【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．

（2）如图（2），将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状并说明理由．

【题目】（12分）某中学组织学生去福利院慰问，在准备礼品时发现，购买1个甲礼品比购买1个乙礼品多花40元，并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等．

（1）求甲、乙两种礼品的单价各为多少元？

（2）学校准备购买甲、乙两种礼品共30个送给福利院的老人，要求购买礼品的总费用不超过2000元，那么最多可购买多少个甲礼品？

【题目】为引导学生广泛阅读文学名著，某校在七年级、八年级开展了读书知识竞赛．该校七、八年级各有学生400人，各随机抽取20名学生进行了抽样调查，获得了他们知识竞赛成绩（分），并对数据进行整理、描述和分析．下面给出了部分信息．

七年级：

74　97　96　89　98　74　65　76　72　78　99　72　97　76　99　74　99　73　98　74

八年级：

76　88　93　65　78　94　89　68　95　50　89　88　89　89　77　94　87　88　92　91

平均数、中位数、众数如表所示：

根据以上信息，回答下列问题：

（1）______，______，______；

（2）该校对读书知识竞赛成绩不少于80分的学生授予“阅读小能手”称号，请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有______人；

（3）结合以上数据，你认为哪个年级读书知识竞赛的总体成绩较好，说明理由．

【题目】如图，在菱形ABCD中，∠B= 60°.

（1）如图①.若点E、F分别在边AB、AD上，且BE=AF，求证:△CEF是等边三角形.

（2）小明发现，当点E、F分别在边AB、AD上，且∠CEF=60°时，△CEF也是等边三角形，

并通过画图验证了猜想;小丽通过探索，认为应该以CE= EF为突破口，构造两个全等三角形:小倩受到小丽的启发，尝试在BC上截取BM =BE，并连接ME，如图②，很快就证明了△CEF是等边三角形.请你根据小倩的方法，写出完整的证明过程.

【题目】如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．

（1）求证：四边形AEDF是菱形；

（2）若∠B=30°，BC=4 ，求四边形AEDF的周长．

【题目】四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是

A．AB∥DC，AD∥BC　　B．AB=DC，AD=BC

C．AO=CO，BO=DO　 　D．AB∥DC，AD=BC

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网