题目内容
【题目】边长分别为6、8、10的三角形的内切圆半径是_____,外接圆半径是_____.
【答案】2, 5
【解析】
先根据勾股定理的逆定理判断出△ABC的形状,设△ABC内切圆的半径为R,切点分别为D、E、F,再根据题意画出图形,先根据正方形的判定定理判断出四边形ODCE是正方形,再根据切线长定理即可得到关于R的一元一次方程,求出R的值即可,再根据直角三角形的外接圆的半径是斜边的一半,得其半径即可.
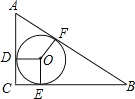
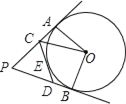
如图所示:△ABC中,AC=6,BC=8,AB=10,
∵62+82=102,即AC2+BC2=AB2,
∴△ABC是直角三角形,
设△ABC内切圆的半径为R,切点分别为D. E.F,
∵CD=CE,BE=BF,AF=AD,
∵OD⊥AC,OE⊥BC,
∴四边形ODCE是正方形,即CD=CE=R,
∴ACCD=ABBF,即6R=10BF①,
BCCE=ABAF,即8R=BF②,
①②联立得,R=2.
∵直角三角形斜边为:10,
∴外接圆半径是:5.
故答案为:2,5.

练习册系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法:①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.⑤不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0.其中说法正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个