题目内容
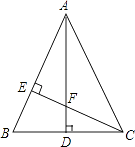
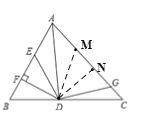
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积________.

【答案】6
【解析】
作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.
作DM=DE交AC于M,作DN⊥AC,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DN,
∵DE=DG,
∴DG=DM,
∴Rt△DEF≌Rt△DMN(HL),
∵DG=DM, DN⊥AC,
∴MN=NG,
∴△DMN≌△DNG,
∵△ADG和△AED的面积分别为48和36,
∴S△MDG=S△ADG-S△ADM=48-36=12,
∴S△DEF=![]() S△MDG=
S△MDG=![]()
![]() 12=6,
12=6,
故答案为:6

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目