题目内容
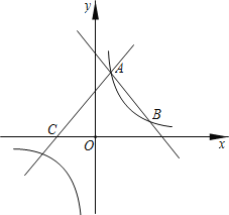
【题目】抛物线y＝ax2+bx+c的部分图象如图，则下列说法：①abc＞0；②b+2a＝0；③b2＞4ac；④a+b+c＜﹣3，正确的是( )
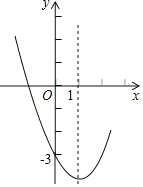
A.①②B.①②③C.①②④D.①②③④
【答案】D
【解析】
根据二次函数y＝ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定解答．
解：由抛物线图象得：开口向上，即a＞0；对称轴﹣
＞0，则b＜0，抛物线与y轴交于负半轴，可得c＜0，abc＞0，故①正确；
∵对称轴﹣＝1，∴b＝﹣2a，
∴b+2a＝0，故②正确；
∵抛物线与x轴有两个交点，
∴b2﹣4ac＞0，
∴b2＞4ac，故③正确；
由抛物线图象可知当x＝1时，y＜﹣3，
∴a+b+c＜﹣3，故④正确；
故选：D．
口算题卡加应用题集训系列答案
综合自测系列答案
【题目】甲、乙两校各有200名体训队队员，为了解这两校体训队员的体能，进行了抽样调查过程如下，请补充完整
收集数据：从甲、乙两个学校各随机抽取20名体课队员，讲行体能测试，测试成绩(百分制)如下：
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据：按如下分数段整理、描述这两组样本数据：
成绩x人数 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲校 | 0 | 0 | 1 | 11 | 7 | 1 |
乙校 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明：成绩80分及以上为体能优秀，70～79分为体能良好，60～69为体能合格，60以下为体能不合格)
分析数据：两组样本数据的平均数、中位数、众数如下表所示
学校 | 平均数 | 中位数 | 众数 | 优秀率 |
甲 | 78.3 | 77.5 | b | 40% |
乙 | 78 | a | 81 | c |
问题解决：(1)直接写出a，b，c的值；
(2)估计甲校90分及以上的学生有多少人．
(3)得出结论：通过以上数据的分析，你认为哪个学校的体训队学生的体能水平更高，并从两个不同的角度说明推断的合理性．
【题目】已知二次函数
中的
，
满足下表
| … |
| 0 | 1 | 2 | 3 | … |
| … | 0 |
|
|
|
| … |
（l）
________，
________；
（2）函数图象对称轴是____________；
（3）如果点
，
是图象上点，则
________；
（4）函数图象与轴交于点
、点
，
是等腰直角三角形，
，则点
坐标为________．
