题目内容
【题目】二次函数y=ax2+bx+c(a≠0)大致的图象如图,关于该二次函数,下列说法错误的是( )
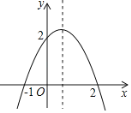
A. 函数有最大值
B. 对称轴是直线x=![]()
C. 当x<![]() 时,y随x的增大而减小
时,y随x的增大而减小
D. 当时﹣1<x<2时,y>0
【答案】C
【解析】
根据函数图象可对A进行判断;利用对称性确定抛物线的对称轴,则可对B进行判断;再根据二次函数的性质对C进行判断;然后利用抛物线在x轴上方所对应的自变量的范围可对D进行判断.
解:A、抛物线的开口向下,所以抛物线有最大值,所以A选项的说法正确;
B、抛物线与x轴交于点(1,0)和(2,0),则抛物线的对称轴为直线x=![]() ,所以B选项的说法正确;
,所以B选项的说法正确;
C、因为抛物线的开口向下,对称轴为直线x=![]() ,则当x<
,则当x<![]() 时,y随x的增大而增大,所以C选项的说法错误;
时,y随x的增大而增大,所以C选项的说法错误;
D、当1<x<2时,y>0,所以D选项的说法正确,
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解某校七年级学生作业时间情况,随机抽取了该校七年级部分学生进行调查,并根据调查结果绘制了如下的统计图.
作业时间分组表(单位:小时)
别 | 作业时间 | 人数 | 频率 |
A | 1≤x≤1.5 | 5 | 0.1 |
B | 1.5≤x≤2 | 20 | b |
C | 2≤x≤2.5 | m | n |
D | x≥2.5 | 7 | 0.14 |
小计 | a | 1 |
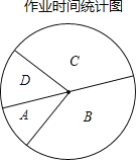
(1)统计图中的a=______;b=______;m=______;n=______.
(2)求出C组的扇形的圆心角度数.
(3)如果该校七年级学生共400名,试估计这400名生作业时间在B组和C组的人数共有多少人?