题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=1,tanC=![]() ,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于![]() BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.
BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.

【答案】![]() .
.
【解析】
过点F作FH⊥AB于点H,证四边形AGFH是正方形,设AG=x,表示出CG,再证△CFG∽△CBA,根据相似比求出x即可.
如图过点F作FH⊥AB于点H,
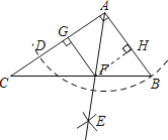
由作图知AD=AB=1,AE平分∠BAC,
∴FG=FH,
又∵∠BAC=∠AGF=90°,
∴四边形AGFH是正方形,
设AG=x,则AH=FH=GF=x,
∵tan∠C=![]() ,
,
∴AC=![]() =
=![]() ,
,
则CG=![]() -x,
-x,
∵∠CGF=∠CAB=90°,
∴FG∥BA,
∴△CFG∽△CBA,
∴![]() ,即
,即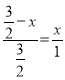 ,
,
解得x=![]() ,
,
∴FG=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目