题目内容
【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动。
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?

【答案】(1)8(2)![]()
【解析】试题分析:(1)根据相遇问题的等量关系列出方程求解即可;
(2)分点M在点E的右边和左边两种情况,根据平行四边形对边相等,利用AN=ME列出方程求解即可.
试题解析:(1)设t秒时两点相遇,
根据题意得,t+2t=2(4+8),解得t=8,
答:经过8秒两点相遇;
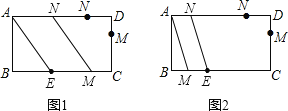
(2)①如图1,点M在E点右侧时,当AN=ME时,四边形AEMN为平行四边形,得:8-t=9-2t,解得t=1,
∵t=1时,点M还在DC上,∴t=1舍去;
②如图2,点M在E点左侧时,当AN=ME时,四边形AEMN为平行四边形,
得:8-t=2t-9,解得t=![]() ,
,
所以,经过![]() 秒钟,点A、E、M、N组成平行四边形.
秒钟,点A、E、M、N组成平行四边形.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目