题目内容
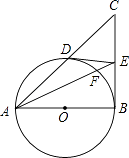
【题目】如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.
(1)求矩形ABCD的面积;
(2)求第1个平行四边形OBB1C的面积是
第2个平行四边形A1B1C1C是
第3个平行四边形O1B1B2C1的面积是
(3)求第n个平行四边形的面积是

【答案】(1)192;(2)96,48,24;(3)192×(![]() )n
)n
【解析】分析:(1)用勾股定理求出BC的长;(2)由图形可知每一个平行四边形的面积都是它前面的平行四边形面积的![]() ,用列举法可得到第n个平行四边形的面积;(3)见(2)中的解析.
,用列举法可得到第n个平行四边形的面积;(3)见(2)中的解析.
详解:
(1)解:∵四边形ABCD是矩形,AC=20,AB=12
∴∠ABC=90°,BC=![]() =
=![]() =16.
=16.
∴S矩形ABCD=AB·BC=12×16=192.
(2)第1个平行四边形OBB1C的面积 192×![]() =96
=96
第2个平行四边形A1B1C1C是 192×![]() ×
×![]() =192×(
=192×(![]() )2=48
)2=48
第3个平行四边形O1B1B2C1的面积是 192×![]() ×
×![]() ×
×![]() =192×(
=192×(![]() )3=24
)3=24
……
第n个平行四边形的面积是 192×(![]() )n.
)n.
(3)由(2)知第n个平行四边形的面积是192×(![]() )n.
)n.

练习册系列答案
相关题目