题目内容
【题目】在正方形ABCD的外侧,作△ADE和△DCF,连接AF、BE.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠ABC=∠BCD=∠CDA=∠DAB=90°)
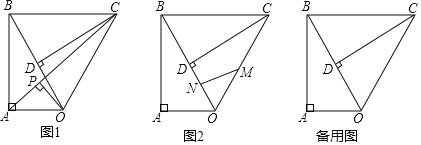
(1)如图①,若△ADE和△DCF是等边三角形,求证:AF=BE,AF⊥BE;
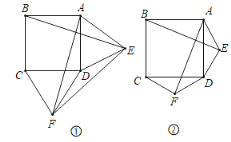
(2)如图②,若△ADE和△DCF为一般三角形,其中AE=DF,ED=FC,则第(1)问中的结论仍然成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)证明见详解;(2)成立,证明见详解
【解析】
(1)根据正方形的性质、等边三角形的性质以及全等三角形的判定定理证明△BAE≌△ADF,根据全等三角形的性质得出结论;
(2)根据边边边定理证明△EAD≌△FDC.根据边角边定理证明△BAE≌△ADF.则BE=AF,∠ABE=∠DAF,与(1)的证明方法相似,可得结论.
解:(1)AF=BE;AF⊥BE.
理由如下:如图①所示:
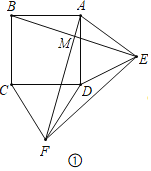
∵四边形ABCD是正方形,
∴∠BAD=∠ADC=90°,AB=AD=CD,
∵△ADE和△DCF是等边三角形,
∴∠DAE=∠CDF=60°,AE=AD,DF=CD,
∴AE=DF,∠BAE=∠ADF=150°,
在△BAE和△ADF中,
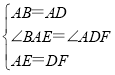
∴△BAE≌△ADF(SAS),
∴AF=BE,∠ABE=∠DAF,
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,
∴AF⊥BE;
故答案为:AF=BE,AF⊥BE.
(2)所画图形如图②,第(1)问的结论成立,理由如下:
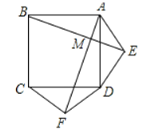
②
在△AED和△DFC中,
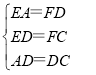
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.即∠BAE=∠ADF.
在△BAE和△ADF中,
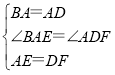
∴△BAE≌△ADF(SAS),
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,
∴AF⊥BE.

 名校课堂系列答案
名校课堂系列答案