[题目]如图.矩形ABCD中.BC=4.CD=2.以AD为直径的半圆O与BC相切于点E.连接BD.则阴影部分的面积为．(结果保留π) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，矩形ABCD中，BC=4，CD=2，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为_____．（结果保留π）

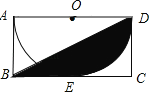
【答案】π

【解析】连接OE，如图，利用切线的性质得OD=2，OE⊥BC，易得四边形OECD为正方形，先利用扇形面积公式，利用S正方形OECD﹣S扇形EOD计算由弧DE、线段EC、CD所围成的面积，然后利用三角形的面积减去刚才计算的面积即可得到阴影部分的面积．

连接OE，如图，

∵以AD为直径的半圆O与BC相切于点E，

∴OD=2，OE⊥BC，

易得四边形OECD为正方形，

∴由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD=22﹣=4﹣π，

∴阴影部分的面积=×2×4﹣（4﹣π）=π，

故答案为：π．

练习册系列答案

【题目】图书馆与学校相距600m，明明从学校出发步行去图书馆，亮亮从图书馆骑车去学校两人同时出发，匀速相向而行，他们与学校的距离S（m）与时间t（s）的图象如图所示：

根据图象回答：

（1）明明步行的速度为　　m/s；亮亮骑车的速度为　　m/s．

（2）分別写出明明、亮亮与学校的距离S1、S2与时间t的关系式．

（3）通过计算求出a的值．

【题目】已知二次函数的图象与轴分别交于点A、B（A左B右），与轴交于点C，顶点是P．

（1）则A点坐标是：________；B点坐标是：________；

（2）当时，如1图所示：设△ACP的面积为，△ABC的面积为，求的值；

（3）当且∠ACB＝45°时，如2图所示：求此二次函数的解析式．

【题目】某中学为促进阳光体育运动发展，计划购进足球、排球充实体育器材，若购买足球30个、排球20个，共需资金2600元，若购买足球40个、排球30个，共需资金3600元．

（1）求足球、排球的价格分别是多少元？

（2）若该校计划购进这两种球的总数是60个，学校至多能够提供资金2800元，求最多能购买足球多少个？

【题目】如图，在Rt△ABC中，∠C＝90°，AB=13，AC=5，BC=12．点O为∠ABC与∠CAB的平分线的交点，则点O到边AB的距离OP为____．

【题目】在正方形ABCD的外侧，作△ADE和△DCF，连接AF、BE．(友情提醒：正方形的四条边都相等，即AB＝BC＝CD＝DA；四个内角都是90°，即∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°)

（1）如图①，若△ADE和△DCF是等边三角形，求证：AF＝BE，AF⊥BE；

（2）如图②，若△ADE和△DCF为一般三角形，其中AE＝DF，ED＝FC，则第（1）问中的结论仍然成立吗?若成立，请给予证明；若不成立，请说明理由．

【题目】随着手机的普及，微信（一种聊天软件）的兴起，许多人抓住这种机会，做起了“微商”很多农产品也改变了原来的销售模式，实行了网上销售，刚大学毕业的小明把自家的冬枣产品也放到了网上，他原计划每天卖斤冬枣，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负单位：斤）；