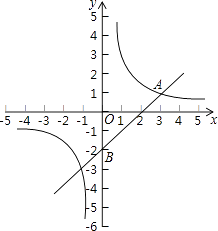题目内容
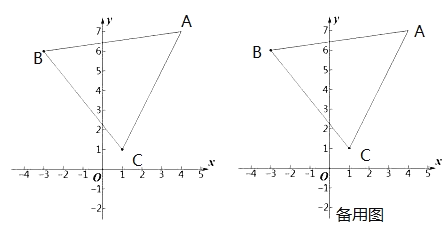
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() 其中
其中![]() 满足:
满足:![]() .
.
(1)![]()
(2)在坐标平面内,将△ABC平移,点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,若平移后E、F两点都在坐标轴上,请直接写出点E的坐标;
(3)若在△ABC内部的![]() 轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
【答案】(1)b=-3,c=1;(2)E(-4,0)或E(0,5);(3)P的坐标为(0,3)或(0,![]() ).
).
【解析】
(1)根据几个非负数和的性质得到b+3=0,c﹣1=0,解方程即可得到结论;
(2)分两种情况讨论:①若B在x轴上,C在y轴上;②若B在y轴上,C在x轴上.根据B、C平移后的点的特征,得出平移方式,即可得出结论;
(3)设P(0,y),其中(1<y<7),根据(2)的两种平移方式分别得出Q的坐标,用割补法求△APQ的面积即可.
(1)由题意得:![]() ,解得:
,解得:![]() ,∴b=-3,c=1.
,∴b=-3,c=1.
(2)∵b=-3,c=1,∴B(-3,6),C(1,1).分两种情况讨论:
①若E在x轴上,F在y轴上,设B(-3,6)平移后为E(a,0),C(1,1)平移后为F(0,b),则平移方式为左1下6,∴E(-4,0);
②若E在y轴上,F在x轴上,设B(-3,6)平移后为E(0,a),C(1,1)平移后为F(b,0),则平移方式为右3下1,∴E(0,5).
综上所述:E(-4,0)或E(0,5).
(3)设P(0,y),其中(1<y<7).分两种情况讨论:
①若平移方式为左1下6,则Q(-1,y-6),如图1.
∵![]() ,∴
,∴![]() =10,解得:y=3,∴P(0,3);
=10,解得:y=3,∴P(0,3);

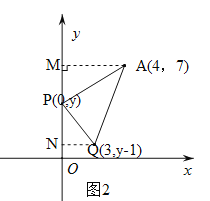
②若平移方式为右3下1,则Q(3,y-1),如图2.
∵![]() ,阿∴
,阿∴![]() =10,解得:y=
=10,解得:y=![]() ,∴P(0,
,∴P(0,![]() ).
).
综上所述:P的坐标为(0,3)或(0,![]() ).
).

【题目】在如图中,每个正方形由边长为1的小正方形组成: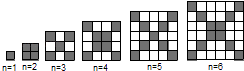
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.