题目内容
【题目】请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中, AD是角平分线.
求证: ![]() .
.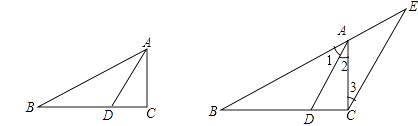
证明:过C作CE∥DA,交BA的延长线于E.
∴ ![]() . ①
. ①![]() AD是角平分线,
AD是角平分线,
∴ ![]() .
.![]()
![]() .
.![]() . ②
. ②
又 ![]() ,
,![]() . ③
. ③![]()
![]() .
.
(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,求BD的长;
(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△ABD和△ACD面积的比来证明三角形内角平分线定理.
【答案】
(1)解:证明过程中用到的定理有:
①平行线的性质定理;
②等腰三角形的判定定理;
③平行线分线段成比例定理
(2)解:∵AD是角平分线,
∴ ![]() ,
,
又∵AB=7cm,AC=4cm,BC=6cm,
∴ ![]() ,
,
∴BD= ![]() (cm)
(cm)
(3)解:∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比= 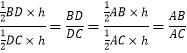 ,
,
可得: ![]()
【解析】(1)利用“平行线的性质定理;等腰三角形的判定定理;平行线分线段成比例定理”可填出答案;(2)学会应用(1)的结论,构造比例式求线段;(3)利用面积法,再结合角平分线性质定理可构造两个比例式,证得结论.
【考点精析】利用三角形的面积和角平分线的性质定理对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目