Question

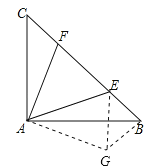
【题目】如图，在等腰直角△ABC的斜边上取异于B，C的两点E，F，使∠EAF=45°，求证：以EF，BE，CF为边的三角形是直角三角形．

Answer 1

【答案】证明见解析.

【解析】试题分析：首先把△ACF绕点A顺时针旋转90°，得到△ABG．连接EG，可得△ACF≌△ABG．进而得到AG=AF，BG=CF，∠ABG=∠ACF=45°，再证明△AEG≌△AEF可得EF=EG，由∠GBE=90°利用勾股定理可得BE2+CF2=EF2，那么根据勾股定理的逆定理得出以EF，BE，CF为边的三角形是直角三角形．

试题解析：证明：把△ACF绕点A顺时针旋转90°，得到△ABG．连接EG．则△ACF≌△ABG，∴AG=AF，BG=CF，∠ABG=∠ACF=45°．∵∠BAC=90°，∠GAF=90°，∴∠GAE=∠EAF=45°．在△AEG和△AEF中，∵，∴△AEG≌△AEF（SAS），∴EG=EF．又∵∠GBE=90°，∴BE2+BG2=EG2，即BE2+CF2=EF2，∴以EF，BE，CF为边的三角形是直角三角形．