题目内容
如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若AB的长为8cm，则图中阴影部分的面积为______cm2．
设AB于小圆切于点C，连接OC，OB．
∵AB于小圆切于点C，
∴OC⊥AB，
∴BC=AC=
AB=
×8=4cm．
∵圆环（阴影）的面积=π•OB2-π•OC2=π（OB2-OC2）
又∵直角△OBC中，OB2=OC2+BC2
∴圆环（阴影）的面积=π•OB2-π•OC2=π（OB2-OC2）=π•BC2=16πcm2．
故答案是：16π．
∵AB于小圆切于点C，
∴OC⊥AB，
∴BC=AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵圆环（阴影）的面积=π•OB2-π•OC2=π（OB2-OC2）
又∵直角△OBC中，OB2=OC2+BC2
∴圆环（阴影）的面积=π•OB2-π•OC2=π（OB2-OC2）=π•BC2=16πcm2．
故答案是：16π．
练习册系列答案
阅读快车系列答案
相关题目
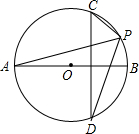
CO交⊙O于点D，连接AD．
