题目内容
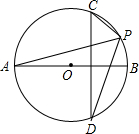
如图,AB是⊙O的直径,弦(非直径)CD⊥AB,P是⊙O上不同于C、D的任一点.
(1)当点P在劣弧CD上运动时,∠APC与∠APD的关系如何?请证明你的结论;
(2)当点P在优弧CD上运动时,∠APC与∠APD的关系如何?请证明你的结论(不要求讨论P点与A点重合的情形)
(1)当点P在劣弧CD上运动时,∠APC与∠APD的关系如何?请证明你的结论;
(2)当点P在优弧CD上运动时,∠APC与∠APD的关系如何?请证明你的结论(不要求讨论P点与A点重合的情形)

∵弦CD⊥AB,AB是直径,
∴弧AC=弧AD;(2分)
∴∠APC=∠APD,(3分)
(2)∠APC+∠APD=180°,
由垂径定理可知
=
,
∴∠APD=∠ADC,
由圆内接四边形的性质可知∠APC+∠ADC=180°,
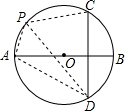
∴∠APC+∠APD=180°(如图中虚线所示).
∴弧AC=弧AD;(2分)
∴∠APC=∠APD,(3分)
(2)∠APC+∠APD=180°,
由垂径定理可知
 |
| AC |
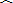 |
| AD |
∴∠APD=∠ADC,
由圆内接四边形的性质可知∠APC+∠ADC=180°,
∴∠APC+∠APD=180°(如图中虚线所示).


练习册系列答案
相关题目