题目内容
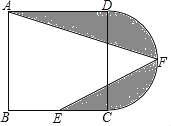
【题目】如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是_________。
【答案】18+18π
【解析】
作FH⊥BC于H，连接AE，如图，根据正方形的性质和切线的性质得BE=CE=CH=FH=6，则利用勾股定理可计算出
，通过Rt△ABE≌△EHF得∠AEF=90°，然后利用图中阴影部分的面积=S正方形ABCD+S半圆-S△ABE-S△AEF进行计算．
解：作FH⊥BC于H，连接AE，如图，
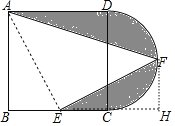
∵点E为BC的中点，点F为半圆的中点，
∴BE=CE=CH=FH=6，
，
易得Rt△ABE≌△EHF，
∴∠AEB=∠EFH，
而∠EFH+∠FEH=90°，
∴∠AEB+∠FEH=90°，
∴∠AEF=90°，
∴图中阴影部分的面积=S正方形ABCD+S半圆-S△ABE-S△AEF
=18+18π．
练习册系列答案
轻松暑假总复习系列答案
相关题目
