题目内容
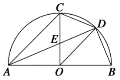
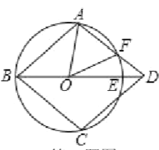
【题目】如图,在![]() 上依次有
上依次有![]() 三点,
三点,![]() 的延长线交
的延长线交![]() 于
于![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() 交
交![]() 于点
于点![]() .连接
.连接![]() , 若
, 若![]() 且
且![]() ,则劣弧
,则劣弧![]() 的长是( )
的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先证明四边形ABCD是菱形,得到AD∥BC;设∠FOE=x,则∠AOF=3x,根据∠ABC+∠BAD=180°,列方程得:4x+2x+![]() (180-3x)=180,求出x的值;然后求CF所对的圆心角和半径的长,最后根据弧长公式即可解答.
(180-3x)=180,求出x的值;然后求CF所对的圆心角和半径的长,最后根据弧长公式即可解答.
解:∵![]()
∴∠CBD=∠ABD
∵CD//AB.
∴∠ABD=∠CDB,
∴∠CBD=∠CDB
∴CB=CD.
∴BE是圆O的直径
∴![]()
∴AB=BC=CD
∵CD//AB
∴.四边形ABCD是菱形
∴AD∥BC
设∠FOE=x,则∠AOF=3x,∠AOD=∠FOE+∠AOF=4x
∵OA=OF.
∴∠OAF=∠OFA=![]() (180-3x)°
(180-3x)°
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD.
∴∠ABC+ ∠BAD=180°
∴4x+2x+![]() (180-3x)=180,解得x=20°
(180-3x)=180,解得x=20°
∴∠AOF=3x=60°,∠AOE=80°
∴∠COF=80°×2-60°=100°
∵OA=OF
∴△AOF是等边三角形
∵OF=AF=2
∴![]() 的长=
的长=![]()
故答案为C.

 阅读快车系列答案
阅读快车系列答案【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
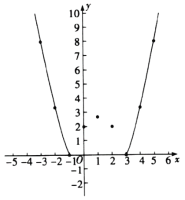
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程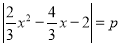 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.