题目内容
【题目】阅读理解：如图1，在△ABC中，当DE∥BC时可以得到三组成比例线段：① 
；② 
；③ 
．反之，当对应线段程比例时也可以推出DE∥BC．
理解运用：三角形的内接四边形是指顶点在三角形各边上的四边形．
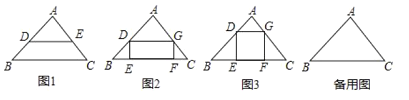
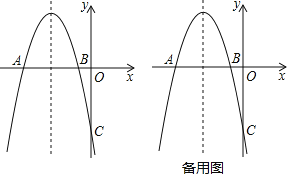
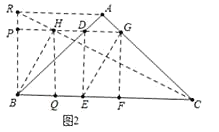
（1）如图2，已知矩形DEFG是△ABC的一个内接矩形，将矩形DEFG沿CB方向向左平移得矩形PBQH，其中顶点D、E、F、G的对应点分别为P、B、Q、H，在图2中画出平移后的图形；
（2）在（1）所得的图形中，连接CH并延长交BP的延长线于点R，连接AR．求证：AR∥BC；
（3）如图3，某小区有一块三角形空地，已知△ABC空地的边AB=400米，BC=600米，∠ABC=45°；准备在△ABC内建一个内接矩形广场DEFG（点E、F在边BC上，点D、G分别在边AB和AC上），三角形其余部分进行植被绿化，按要求欲使矩形DEFG的对角线EG最短，请在备用图中画出使对角线EG最短的矩形．并求出对角线EG的最短距离（不要求证明）．
【答案】（1）见解析；（2）见解析；（3）图形见解析，最短距离为
【解析】
（1）根据题意，利用平移的性质画出矩形PBQH即可；
（2）如图1中，连接CH并延长交BP的延长线于点R，连接AR，利用平行线分线段成比例，由PH∥BC，DG∥BC，可得对应线段成比例，再由PH=DG可证RH，BC，AG，AC四条线段对应成比例，可得到AR∥GH，再由HG∥BC，利用平行线的传递性，可证得结论；
（3）如图2中，作AR∥BC．BR⊥BC，连接CR，作BH⊥CR，过点H作PH∥BC交RB于P交AB于D交AC于G，作HQ⊥BC于Q，DE⊥BC于E，GF⊥BC于F ，易得到四边形DEFG是矩形，此时矩形的对角线最短即就是EG的长，利用勾股定理求出GR的长，再求出BH的长，然后利用平行四边形的对边相等，可求出EG的长．
（1）解：矩形PBQH如图1所示
（2）解：如图1中，连接CH并延长交BP的延长线于点R，连接AR
∵PH∥BC，
∴ 
∵DG∥BC，
∴ 
∵PH=DG，
∴ 
∴AR∥HG，
∵HG∥BC，
∴AR∥BC
（3）解：如图2中，作AR∥BC．BR⊥BC，连接CR，作BH⊥CR，过点H作PH∥BC交RB于P交AB于D交AC于G，作HQ⊥BC于Q，DE⊥BC于E，GF⊥BC于F
则四边形DEFG是矩形，此时矩形的对角线最短（BH是垂线段，垂线段最短，易证EG=BH，故此时矩形的对角线EG最短）．
在Rt△RBC中，
∵BC=600，BR=200
∴CR=
∴BH=
由（2）可知EG=BH=
．
