题目内容
【题目】为丰富学生的文体生活,某学校准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查,在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
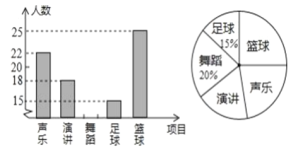
(1)被抽查的学生一共有人__________;
(2)将条形统计图补充完整;
(3)若全校有学生1500人,请你估计全校有意参加“声乐”杜团的学生人数;
(4)在“舞蹈社团”活动中,甲、乙、丙、丁、戊五位同学表现优秀,现决定从这五位同学中任选两位参加“元旦迎新汇演”,请用列表或画树状图的方法求出恰好选中甲、乙两位同学的概率.
【答案】(1)100;(2)详见解析;(3)330;(4)![]() .
.
【解析】
(1)根据参加足球社团总人数为15人及所占比例为15%,作除法运算即可得出总人数
(2)用随机抽取的总人数减去参加声乐、演讲、足球、篮球社团的人数,即可得出参加舞蹈社团的人数,据此补全统计图即可;
(3)全校学生总人数乘以参加声乐社团人数占抽查人数的比例即可得出答案;
(4)直接列表求概率即可.
解:(1)![]() (人)
(人)
(2)有意参加“舞蹈”社团的人数为![]() (人)
(人)
补全条形统计图如下:
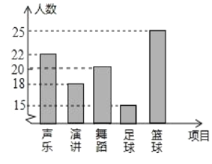
(3)![]() (人).
(人).
答:估计全校有意参加“声乐”社团的学生人数有330人.
(4)列表得:
甲 | 乙 | 丙 | 丁 | 戊 | |
甲 | (甲,乙) | (甲,丙) | (甲,丁) | (甲,戊) | |
乙 | (乙,甲) | (乙,丙) | (乙,丁) | (乙,戊) | |
丙 | (丙,甲) | (丙,乙) | (丙,丁) | (丙,戊) | |
丁 | (丁,甲) | (丁,乙) | (丁,丙) | (丁,戊) | |
戊 | (戊,甲) | (戊,乙) | (戊,丙) | (戊,丁) |
由表格可知,所有可能出现的结果共有20种,且每种结果出现的可能性相同,其中恰好选中甲、乙两位同学的结果有2种.
∴![]() (恰好选中甲、乙两位同学)
(恰好选中甲、乙两位同学)![]() .
.

【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.