题目内容
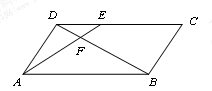
如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD,且AE、BD交于点F,则S△DEF:S△ADF:S△BAF等于( )

| A.4:10:25 | B.4:9:25 | C.2:3:5 | D.2:5:25 |
B.
试题分析:根据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的面积比等于相似比的平方就可得到答案.
∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DFE∽△BFA,
∴
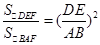 .
.∵DE:EC=2:3,
∴DE:DC=DE:AB=2:5,
∴S△DEF:S△ABF=4:25
同理可证:S△DEF:S△ADF=4:9
∴S△DEF:S△ADF:S△ABF=4:9:25.
故选B.
考点: 1.相似三角形的判定与性质;2.平行四边形的性质.

练习册系列答案
相关题目
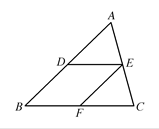

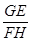 的值.
的值. 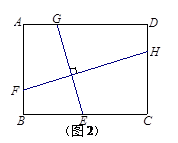
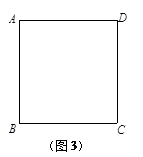
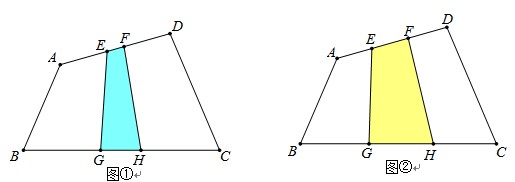
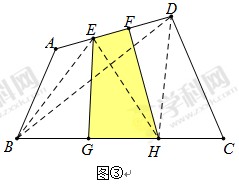
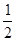 S△EBH
S△EBH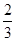 S△ABD
S△ABD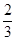 S四边形ABCD
S四边形ABCD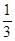 S四边形ABCD
S四边形ABCD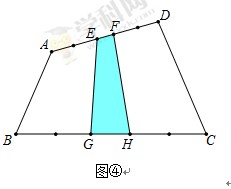
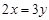 ,那么
,那么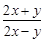 = .
= .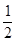 ,则点的对应点′的坐标是
,则点的对应点′的坐标是