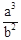题目内容
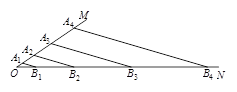
如图,点A1、A2、A3、…,点B1、B2、B3、…,分别在射线OM、ON上,A1B1∥A2B2∥A3B3∥A4B4∥….如果A1B1=2,A1A2=2OA1,A2A3=3OA1,A3A4=4OA1,….那么A2B2= ,AnBn= .(n为正整数)

6;n(n+1).
试题分析:根据OA1=1,求出A1A2、A2A3、A3A4的值,推出AnAn-1的值,根据平行线分线段成比例定理得出
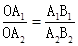 ,代入求出A2B2=6=2×(2+1),A3B3=12=3×(3+1),A4B4=20=4(4+1),推出AnBn=n(n+1)即可:∵OA1=1,
,代入求出A2B2=6=2×(2+1),A3B3=12=3×(3+1),A4B4=20=4(4+1),推出AnBn=n(n+1)即可:∵OA1=1,∴A1A2=2×1=2,
A2A3=3×1=3,
A3A4=4,
…
An-2An-1=n-1,
An-1An=n,
∵A1B1∥A2B2∥A3B3∥A4B4∥…,
∴
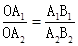 ,
,∴
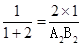 ,
,∴A2B2=6=2×(2+1),
A3B3=12=3×(3+1),
A4B4=20=4(4+1),
…
∴AnBn=n(n+1),
故答案为:6,n(n+1).

练习册系列答案
相关题目
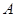 的坐标为
的坐标为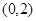 ,点
,点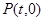 在
在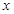 轴上,
轴上,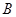 是线段
是线段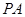 的中点.将线段
的中点.将线段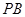 绕着点
绕着点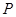 顺时针方向旋转
顺时针方向旋转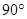 ,得到线段
,得到线段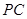 ,连结
,连结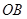 、
、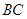 .
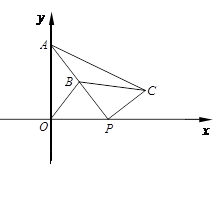
.
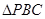 的形状,并简要说明理由;
的形状,并简要说明理由;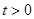 时,试问:以
时,试问:以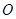 、
、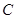 为顶点的四边形能否为平行四边形?若能,求出相应的
为顶点的四边形能否为平行四边形?若能,求出相应的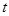 的值?若不能,请说明理由;
的值?若不能,请说明理由;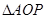 与
与 相似?
相似? ,则
,则 ____________.
____________.