题目内容
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
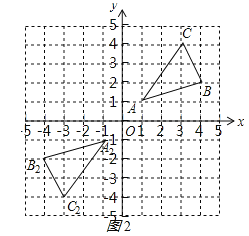
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

【答案】(1)见解析;(2)见解析;(3)P(2,0).
【解析】
(1)根据网格结构找出点A、B、C平移后的对应点的位置,然后顺次连接即可;
(2))找出点A、B、C关于原点O的对称点的位置,然后顺次连接即可;
(3)找出A的对称点A′,连接BA′,与x轴交点即为P.
解:(1)根据网格结构找出点A、B、C平移后的对应点的位置,然后顺次连接,如图所示:
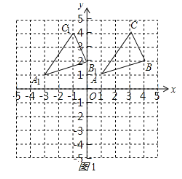
(2)找出点A、B、C关于原点O的对称点的位置,然后顺次连接,如图所示:
(3)找出A的对称点A′,连接BA′,与x轴交点即为P,
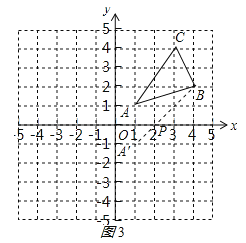 ,
,
由题知,A(1,1),B(4,2),
∴A′(1,-1),
设A′B的解析式为y=kx+b,把B(4,2),A′(1,-1)代入y=kx+b中,
则![]() ,
,
解得:![]() ,
,
∴y=x-2,
当y=0时,x=2,
则P点坐标为(2,0).

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目





