Question

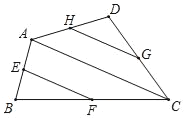
【题目】如图，△ABC中，∠ACB=90°，∠A=30°，将△ABC绕C点按逆时针方向旋转α角（0°＜α＜90°）得到△DEC，设CD交AB于F，连接AD，当旋转角α度数为____________，△ADF是等腰三角形.

Answer 1

【答案】40°或20°．

【解析】

根据旋转的性质得∠DCA＝α，CD＝CA，则∠CDA＝∠CAD＝（180°α）＝90°α，利用三角形外角的性质得∠DFA＝30°＋α，当△ADF是等腰三角形，若FD＝FA，则∠FDA＝∠FAD，不合题意；然后讨论AF＝AD或DF＝DA，分别利用等腰三角形的性质得到90°α＝30°＋α；30°＋α＝90°α30°，即可得到α的值．

解：∵△ABC绕C点按逆时针方向旋转α角（0°＜α＜90°）得到△DEC，

∴∠DCA＝α，CD＝CA，

∴∠CDA＝∠CAD＝（180°α）＝90°α，

∵△ADF是等腰三角形，∠DFA＝30°＋α，

①当FD＝FA，则∠FDA＝∠FAD，不合题意，舍去；

②当AF＝AD，则∠ADF＝∠AFD，

∴90°α＝30°＋α，

解得α＝40°；

③当DF＝DA，则∠DFA＝∠DAF，

∴30°＋α＝90°α30°，

解得α＝20°，

故答案为40°或20°．