题目内容
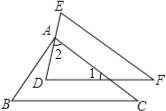
【题目】如图，已知△ABC≌△DEF，DF∥BC，且∠B＝60°，∠F＝40°，点A在DE上，则∠BAD的度数为_________°．
【答案】20°
【解析】
先由△ABC≌△DEF，根据全等三角形的性质得出∠B=∠E=60°，∠C=∠F=40°，由DF∥BC，得出∠1=∠C，等量代换得到∠1=∠F，那么AC∥EF，于是∠2=∠E=60°．由三角形内角和定理求出∠BAC=180°-∠B-∠C=80°，于是∠BAD=∠BAC-∠2=20°．
∵△ABC≌△DEF，
∴∠B=∠E=60°，∠C=∠F=40°，
∵DF∥BC，
∴∠1=∠C，
∴∠1=∠F，
∴AC∥EF，
∴∠2=∠E=60°，
∵∠BAC=180°-∠B-∠C=180°-60°-40°=80°，
∴∠BAD=∠BAC-∠2=80°-60°=20°，
故答案为：20.
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
