题目内容
【题目】如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则PB:P′A的值为 . 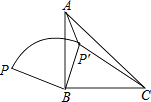
【答案】1:2
【解析】解:如图,连接AP, ∵BP绕点B顺时针旋转90°到BP′,
∴BP=BP′,∠ABP+∠ABP′=90°,
又∵△ABC是等腰直角三角形,
∴AB=BC,∠CBP′+∠ABP′=90°,
∴∠ABP=∠CBP′,
在△ABP和△CBP′中,
∵ 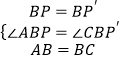 ,
,
∴△ABP≌△CBP′(SAS),
∴AP=P′C,
∵P′A:P′C=1:3,
∴AP=3P′A,
连接PP′,则△PBP′是等腰直角三角形,
∴∠BP′P=45°,PP′= ![]() PB,
PB,
∵∠AP′B=135°,
∴∠AP′P=135°﹣45°=90°,
∴△APP′是直角三角形,
设P′A=x,则AP=3x,
根据勾股定理,PP′= ![]() =
= ![]() =2
=2 ![]() x,
x,
∴PP′= ![]() PB=2
PB=2 ![]() x,
x,
解得PB=2x,
∴P′A:PB=x:2x=1:2.
故答案是:1:2.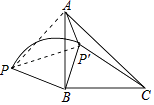
【考点精析】通过灵活运用等腰直角三角形和旋转的性质,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需 ![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需 ![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围); 表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 | 2800 | ||
精加工获利/元 | 25800 |
y与x的函数关系式
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?