题目内容
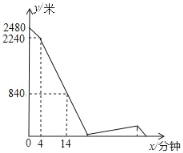
【题目】A、B两地之间的路程为2480米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是___米.
【答案】300.
【解析】
利用速度=路程÷时间可求出甲、乙的速度,由二者相遇的时间=4+A、B两地之间的路程÷二者速度和,可求出二者相遇的时间,再由A、C两地之间的距离=甲的速度×二者相遇的时间可求出A、C两地之间的距离,由A、C两地之间的距离结合甲、乙的速度,可求出乙到达A地时甲与A地相距的路程.
甲的速度为(2480﹣2240)÷4=60(米/分钟),
乙的速度为(2240﹣840)÷(14﹣4)﹣60=80(米/分钟),
甲、乙相遇的时间为4+2240÷(60+80)=20(分钟),
A、C两地之间的距离为60×20=1200(米),
乙到达A地时,甲与A地相距的路程为1200﹣1200÷80×60=300(米).
故答案为:300.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目